Mutual Information Learned Classifiers: an Information-theoretic Viewpoint of Training Deep Learning Classification Systems
Paper and Code
Oct 03, 2022

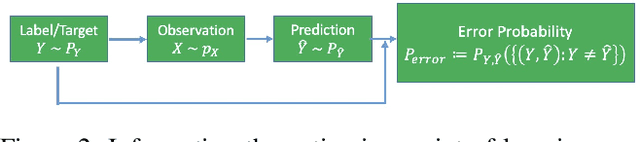

Deep learning systems have been reported to acheive state-of-the-art performances in many applications, and one of the keys for achieving this is the existence of well trained classifiers on benchmark datasets which can be used as backbone feature extractors in downstream tasks. As a main-stream loss function for training deep neural network (DNN) classifiers, the cross entropy loss can easily lead us to find models which demonstrate severe overfitting behavior when no other techniques are used for alleviating it such as data augmentation. In this paper, we prove that the existing cross entropy loss minimization for training DNN classifiers essentially learns the conditional entropy of the underlying data distribution of the dataset, i.e., the information or uncertainty remained in the labels after revealing the input. In this paper, we propose a mutual information learning framework where we train DNN classifiers via learning the mutual information between the label and input. Theoretically, we give the population error probability lower bound in terms of the mutual information. In addition, we derive the mutual information lower and upper bounds for a concrete binary classification data model in $\mbR^n$, and also the error probability lower bound in this scenario. Besides, we establish the sample complexity for accurately learning the mutual information from empirical data samples drawn from the underlying data distribution. Empirically, we conduct extensive experiments on several benchmark datasets to support our theory. Without whistles and bells, the proposed mutual information learned classifiers (MILCs) acheive far better generalization performances than the state-of-the-art classifiers with an improvement which can exceed more than 10\% in testing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge