Multi-Objective Learning to Predict Pareto Fronts Using Hypervolume Maximization
Paper and Code
Feb 08, 2021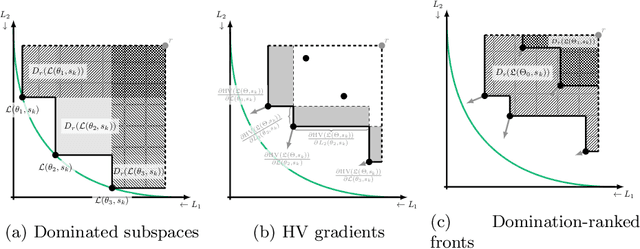
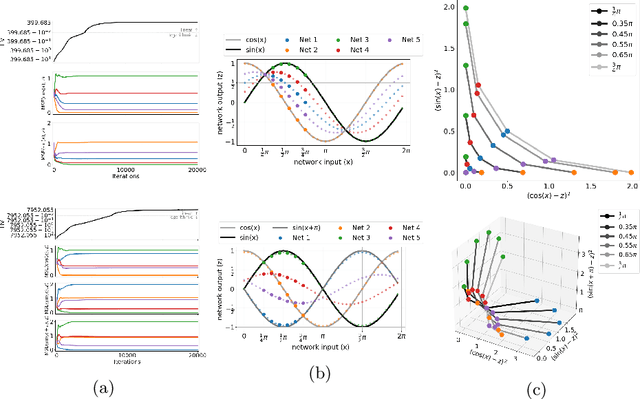
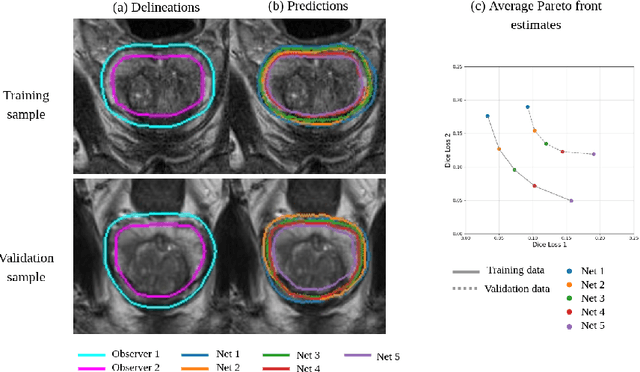
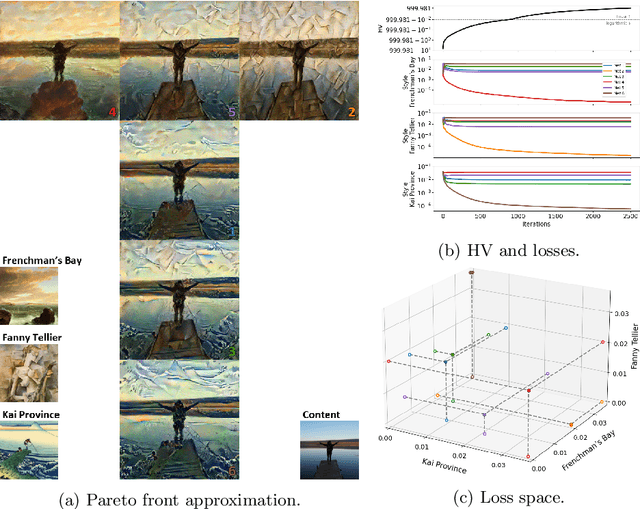
Real-world problems are often multi-objective with decision-makers unable to specify a priori which trade-off between the conflicting objectives is preferable. Intuitively, building machine learning solutions in such cases would entail providing multiple predictions that span and uniformly cover the Pareto front of all optimal trade-off solutions. We propose a novel learning approach to estimate the Pareto front by maximizing the dominated hypervolume (HV) of the average loss vectors corresponding to a set of learners, leveraging established multi-objective optimization methods. In our approach, the set of learners are trained multi-objectively with a dynamic loss function, wherein each learner's losses are weighted by their HV maximizing gradients. Consequently, the learners get trained according to different trade-offs on the Pareto front, which otherwise is not guaranteed for fixed linear scalarizations or when optimizing for specific trade-offs per learner without knowing the shape of the Pareto front. Experiments on three different multi-objective tasks show that the outputs of the set of learners are indeed well-spread on the Pareto front. Further, the outputs corresponding to validation samples are also found to closely follow the trade-offs that were learned from training samples for our set of benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge