Multi-dueling Bandits with Dependent Arms
Paper and Code
Apr 29, 2017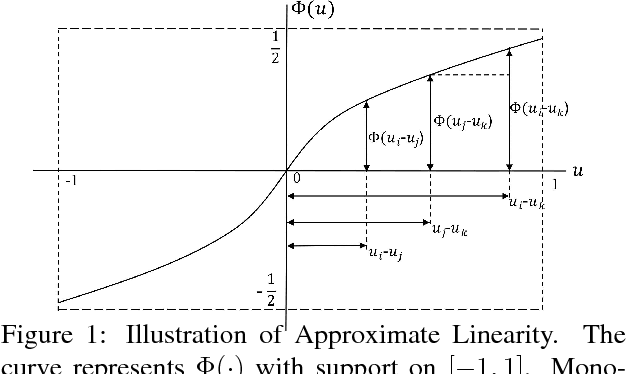

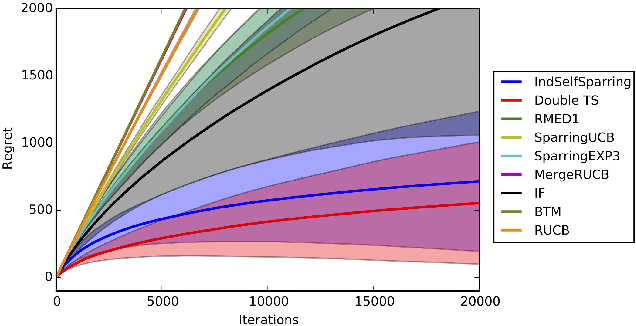
The dueling bandits problem is an online learning framework for learning from pairwise preference feedback, and is particularly well-suited for modeling settings that elicit subjective or implicit human feedback. In this paper, we study the problem of multi-dueling bandits with dependent arms, which extends the original dueling bandits setting by simultaneously dueling multiple arms as well as modeling dependencies between arms. These extensions capture key characteristics found in many real-world applications, and allow for the opportunity to develop significantly more efficient algorithms than were possible in the original setting. We propose the \selfsparring algorithm, which reduces the multi-dueling bandits problem to a conventional bandit setting that can be solved using a stochastic bandit algorithm such as Thompson Sampling, and can naturally model dependencies using a Gaussian process prior. We present a no-regret analysis for multi-dueling setting, and demonstrate the effectiveness of our algorithm empirically on a wide range of simulation settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge