Multi-consensus Decentralized Accelerated Gradient Descent

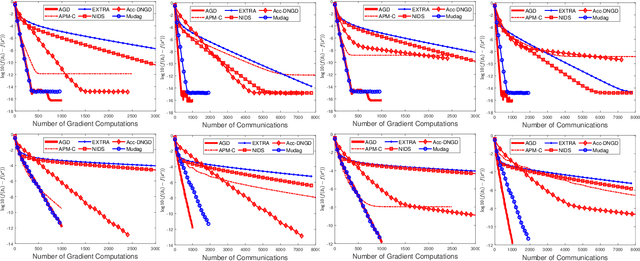
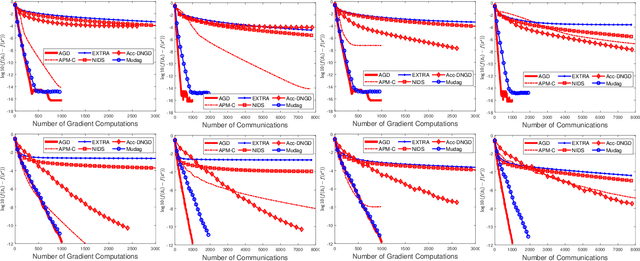
This paper considers the decentralized optimization problem, which has applications in large scale machine learning, sensor networks, and control theory. We propose a novel algorithm that can achieve near optimal communication complexity, matching the known lower bound up to a logarithmic factor of the condition number of the problem. Our theoretical results give affirmative answers to the open problem on whether there exists an algorithm that can achieve a communication complexity (nearly) matching the lower bound depending on the global condition number instead of the local one. Moreover, the proposed algorithm achieves the optimal computation complexity matching the lower bound up to universal constants. Furthermore, to achieve a linear convergence rate, our algorithm \emph{doesn't} require the individual functions to be (strongly) convex. Our method relies on a novel combination of known techniques including Nesterov's accelerated gradient descent, multi-consensus and gradient-tracking. The analysis is new, and may be applied to other related problems. Empirical studies demonstrate the effectiveness of our method for machine learning applications.