Motion Planning under Partial Observability using Game-Based Abstraction

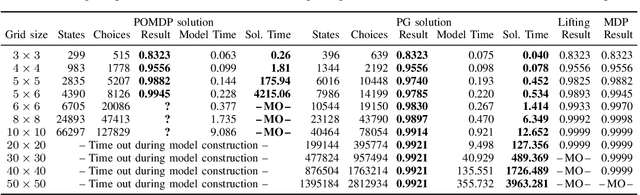
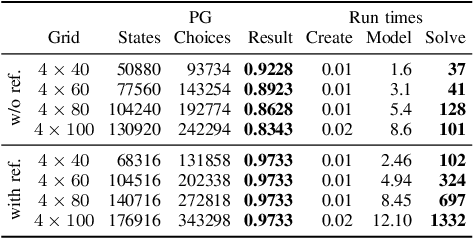
We study motion planning problems where agents move inside environments that are not fully observable and subject to uncertainties. The goal is to compute a strategy for an agent that is guaranteed to satisfy certain safety and performance specifications. Such problems are naturally modelled by partially observable Markov decision processes (POMDPs). Because of the potentially huge or even infinite belief space of POMDPs, verification and strategy synthesis is in general computationally intractable. We tackle this difficulty by exploiting typical structural properties of such scenarios; for instance, we assume that agents have the ability to observe their own positions inside an environment. Ambiguity in the state of the environment is abstracted into non-deterministic choices over the possible states of the environment. Technically, this abstraction transforms POMDPs into probabilistic two-player games (PGs). For these PGs, efficient verification tools are able to determine strategies that approximate certain measures on the POMDP. If an approximation is too coarse to provide guarantees, an abstraction refinement scheme further resolves the belief space of the POMDP. We demonstrate that our method improves the state of the art by orders of magnitude compared to a direct solution of the POMDP.