Modularity Trumps Invariance for Compositional Robustness
Paper and Code
Jun 15, 2023
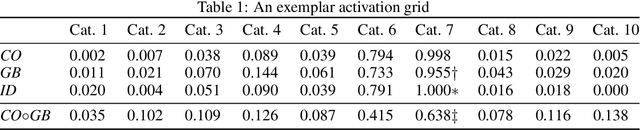
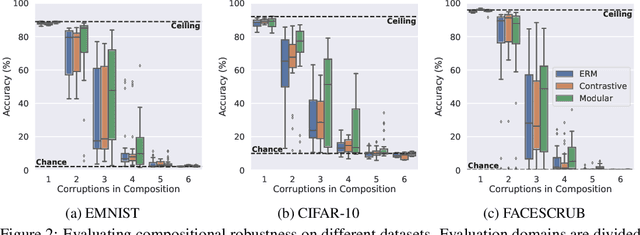
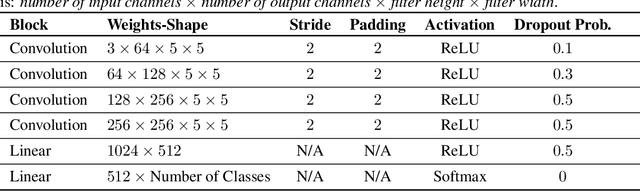
By default neural networks are not robust to changes in data distribution. This has been demonstrated with simple image corruptions, such as blurring or adding noise, degrading image classification performance. Many methods have been proposed to mitigate these issues but for the most part models are evaluated on single corruptions. In reality, visual space is compositional in nature, that is, that as well as robustness to elemental corruptions, robustness to compositions of corruptions is also needed. In this work we develop a compositional image classification task where, given a few elemental corruptions, models are asked to generalize to compositions of these corruptions. That is, to achieve compositional robustness. We experimentally compare empirical risk minimization with an invariance building pairwise contrastive loss and, counter to common intuitions in domain generalization, achieve only marginal improvements in compositional robustness by encouraging invariance. To move beyond invariance, following previously proposed inductive biases that model architectures should reflect data structure, we introduce a modular architecture whose structure replicates the compositional nature of the task. We then show that this modular approach consistently achieves better compositional robustness than non-modular approaches. We additionally find empirical evidence that the degree of invariance between representations of 'in-distribution' elemental corruptions fails to correlate with robustness to 'out-of-distribution' compositions of corruptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge