Model-Based Real-Time Motion Tracking using Dynamical Inverse Kinematics

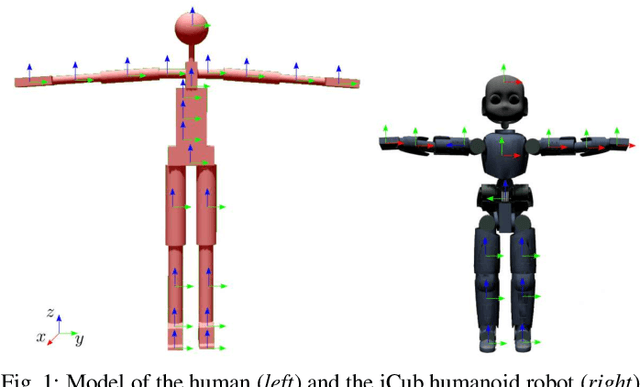
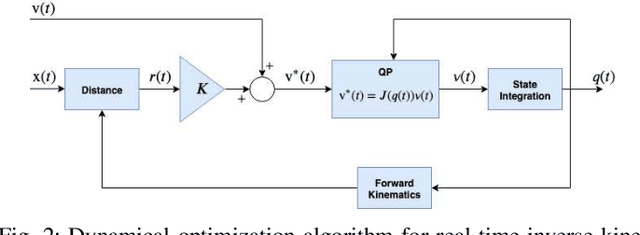
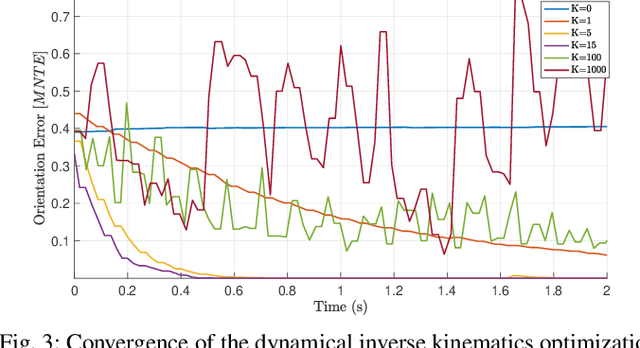
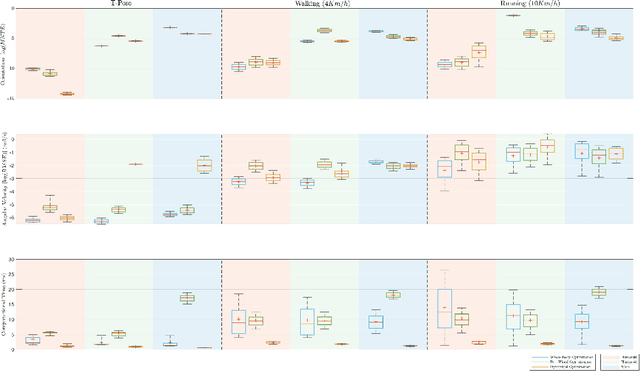
This paper contributes towards the development of motion tracking algorithms for time-critical applications, proposing an infrastructure for solving dynamically the inverse kinematics of human models. We present a method based on the integration of the differential kinematics, and for which the convergence is proved using Lyapunov analysis. The method is tested in an experimental scenario where the motion of a subject is tracked in static and dynamic configurations, and the inverse kinematics is solved both for human and humanoid models. The architecture is evaluated both terms of accuracy and computational load, and compared to iterative optimization algorithms.