Meta-Learning for Adaptive Filters with Higher-Order Frequency Dependencies
Paper and Code
Sep 20, 2022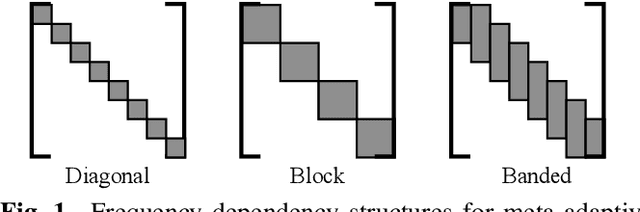
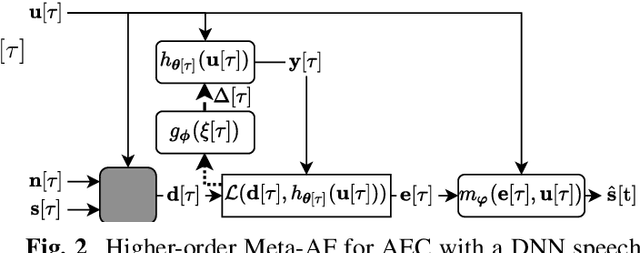
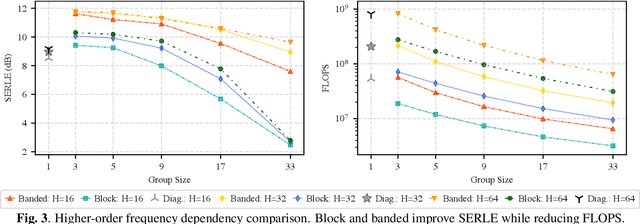
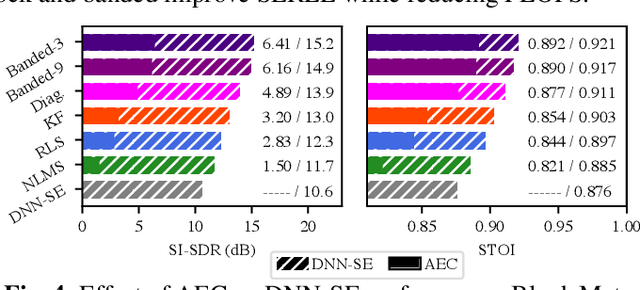
Adaptive filters are applicable to many signal processing tasks including acoustic echo cancellation, beamforming, and more. Adaptive filters are typically controlled using algorithms such as least-mean squares(LMS), recursive least squares(RLS), or Kalman filter updates. Such models are often applied in the frequency domain, assume frequency independent processing, and do not exploit higher-order frequency dependencies, for simplicity. Recent work on meta-adaptive filters, however, has shown that we can control filter adaptation using neural networks without manual derivation, motivating new work to exploit such information. In this work, we present higher-order meta-adaptive filters, a key improvement to meta-adaptive filters that incorporates higher-order frequency dependencies. We demonstrate our approach on acoustic echo cancellation and develop a family of filters that yield multi-dB improvements over competitive baselines, and are at least an order-of-magnitude less complex. Moreover, we show our improvements hold with or without a downstream speech enhancer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge