Merge Double Thompson Sampling for Large Scale Online Ranker Evaluation

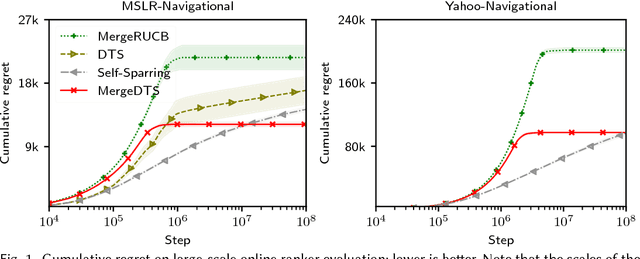
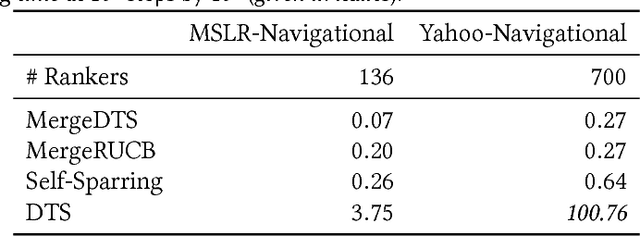
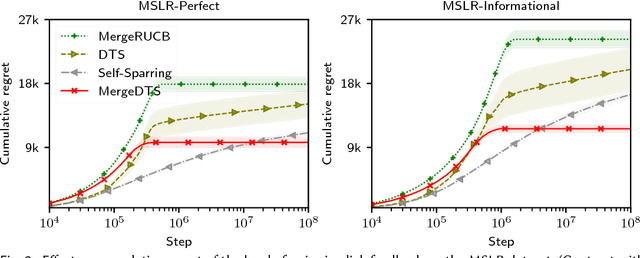
Online ranker evaluation is one of the key challenges in information retrieval. While the preferences of rankers can be inferred by interleaved comparison methods, how to effectively choose the pair of rankers to generate the result list without degrading the user experience too much can be formalized as a K-armed dueling bandit problem, which is an online partial-information learning framework, where feedback comes in the form of pair-wise preferences. A commercial search system may evaluate a large number of rankers concurrently, and scaling effectively in the presence of numerous rankers has not been fully studied. In this paper, we focus on solving the large-scale online ranker evaluation problem under the so-called Condorcet assumption, where there exists an optimal ranker that is preferred to all other rankers. We propose Merge Double Thompson Sampling (MergeDTS), which first utilizes a divide-and-conquer strategy that localizes the comparisons carried out by the algorithm to small batches of rankers, and then employs the Thompson Sampling (TS) to reduce the comparisons between suboptimal rankers inside these small batches. The effectiveness (regret) and efficiency (time complexity) of MergeDTS are extensively evaluated using examples from the domain of online evaluation for web search. Our main finding is that for large-scale Condorcet ranker evaluation problems MergeDTS outperforms the state-of-the-art dueling bandit algorithms.