Memorized Sparse Backpropagation

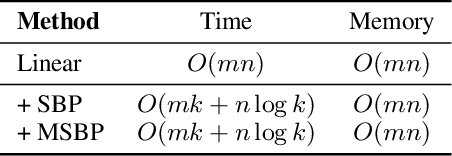
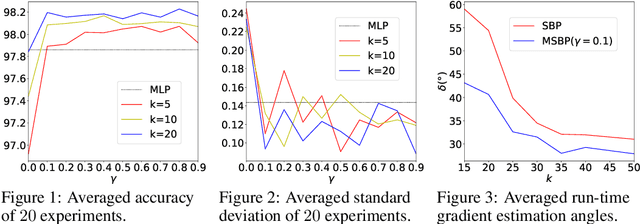
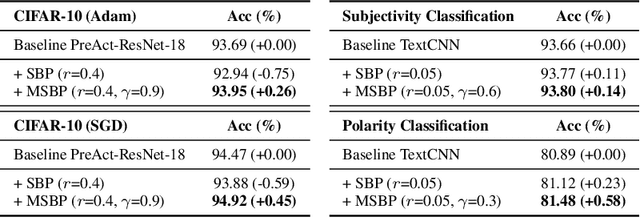
Neural network learning is typically slow since backpropagation needs to compute full gradients and backpropagate them across multiple layers. Despite its success of existing work in accelerating propagation through sparseness, the relevant theoretical characteristics remain unexplored and we empirically find that they suffer from the loss of information contained in unpropagated gradients. To tackle these problems, in this work, we present a unified sparse backpropagation framework and provide a detailed analysis of its theoretical characteristics. Analysis reveals that when applied to a multilayer perceptron, our framework essentially performs gradient descent using an estimated gradient similar enough to the true gradient, resulting in convergence in probability under certain conditions. Furthermore, a simple yet effective algorithm named memorized sparse backpropagation (MSBP) is proposed to remedy the problem of information loss by storing unpropagated gradients in memory for the next learning. The experiments demonstrate that the proposed MSBP is able to effectively alleviate the information loss in traditional sparse backpropagation while achieving comparable acceleration.