Measuring axiomatic soundness of counterfactual image models
Paper and Code
Mar 02, 2023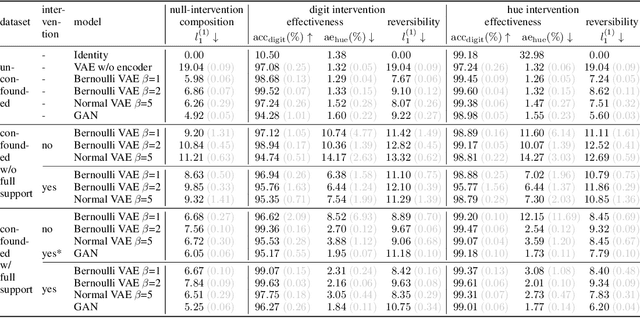

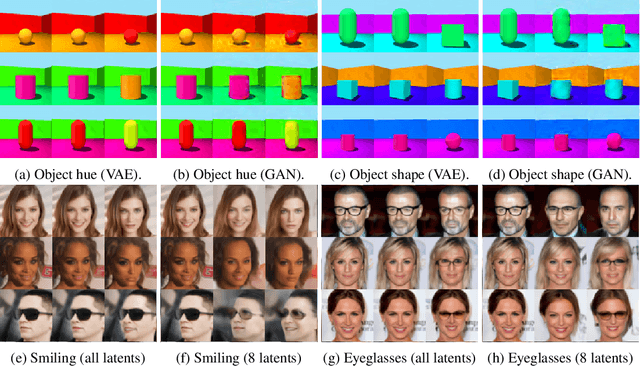
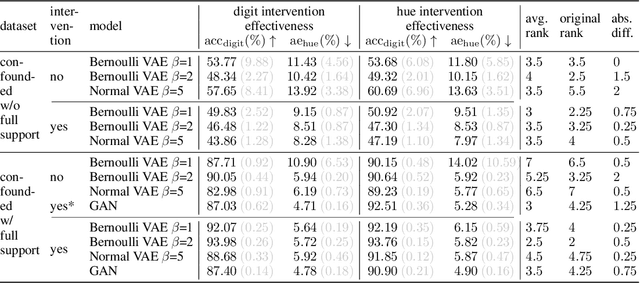
We present a general framework for evaluating image counterfactuals. The power and flexibility of deep generative models make them valuable tools for learning mechanisms in structural causal models. However, their flexibility makes counterfactual identifiability impossible in the general case. Motivated by these issues, we revisit Pearl's axiomatic definition of counterfactuals to determine the necessary constraints of any counterfactual inference model: composition, reversibility, and effectiveness. We frame counterfactuals as functions of an input variable, its parents, and counterfactual parents and use the axiomatic constraints to restrict the set of functions that could represent the counterfactual, thus deriving distance metrics between the approximate and ideal functions. We demonstrate how these metrics can be used to compare and choose between different approximate counterfactual inference models and to provide insight into a model's shortcomings and trade-offs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge