Majority Vote for Distributed Differentially Private Sign Selection
Paper and Code
Sep 08, 2022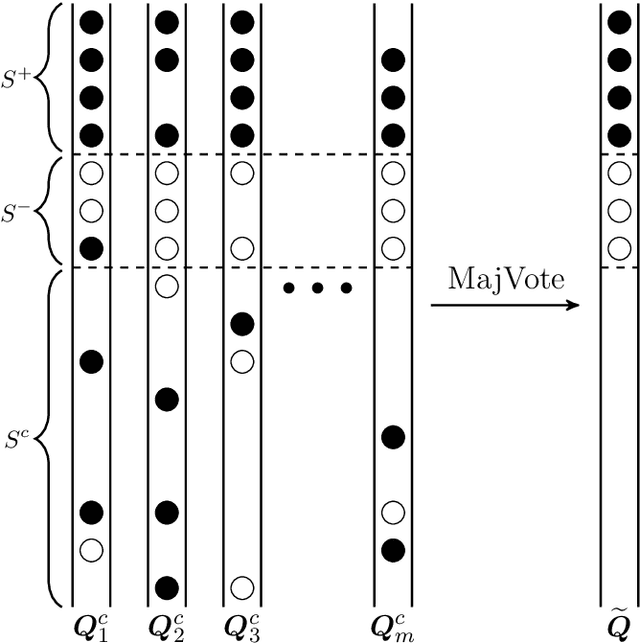
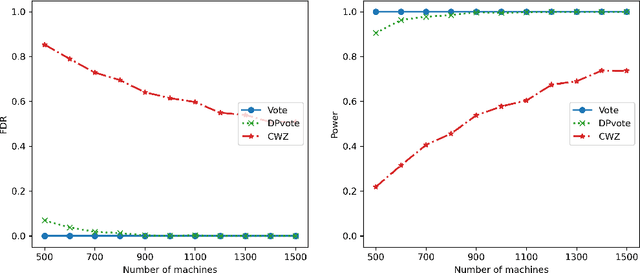
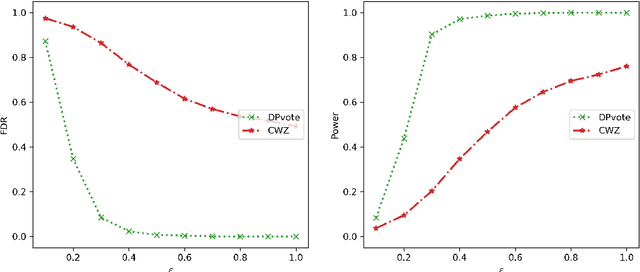
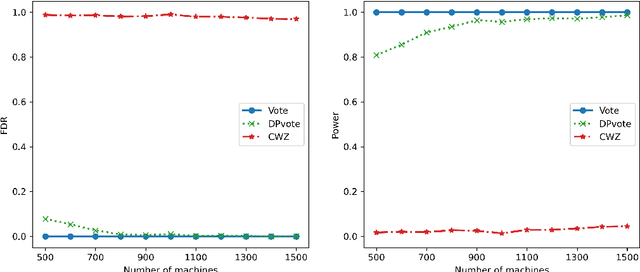
Privacy-preserving data analysis has become prevailing in recent years. In this paper, we propose a distributed group differentially private majority vote mechanism for the sign selection problem in a distributed setup. To achieve this, we apply the iterative peeling to the stability function and use the exponential mechanism to recover the signs. As applications, we study the private sign selection for mean estimation and linear regression problems in distributed systems. Our method recovers the support and signs with the optimal signal-to-noise ratio as in the non-private scenario, which is better than contemporary works of private variable selections. Moreover, the sign selection consistency is justified with theoretical guarantees. Simulation studies are conducted to demonstrate the effectiveness of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge