Lower Bounds and Conditioning of Differentiable Games
Paper and Code
Jun 17, 2019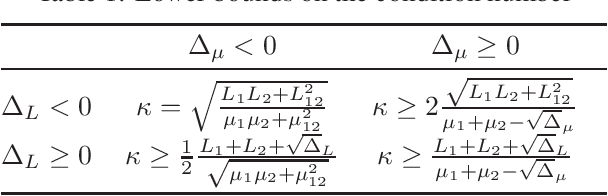



Many recent machine learning tools rely on differentiable game formulations. While several numerical methods have been proposed for these types of games, most of the work has been on convergence proofs or on upper bounds for the rate of convergence of those methods. In this work, we approach the question of fundamental iteration complexity by providing lower bounds. We generalise Nesterov's argument -- used in single-objective optimisation to derive a lower bound for a class of first-order black box optimisation algorithms -- to games. Moreover, we extend to games the p-SCLI framework used to derive spectral lower bounds for a large class of derivative-based single-objective optimisers. Finally, we propose a definition of the condition number arising from our lower bound analysis that matches the conditioning observed in upper bounds. Our condition number is more expressive than previously used definitions, as it covers a wide range of games, including bilinear games that lack strong convex-concavity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge