Low-Latency Federated Learning over Wireless Channels with Differential Privacy
Paper and Code
Jun 20, 2021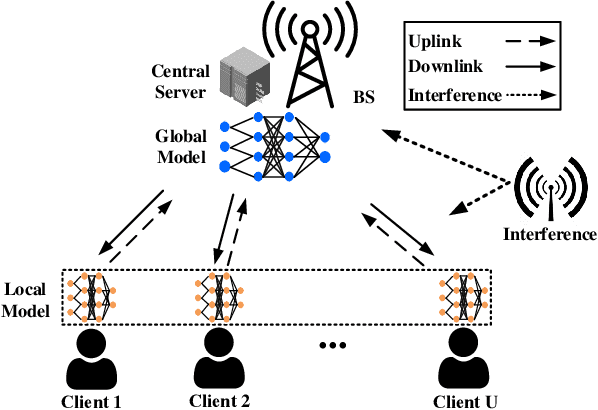
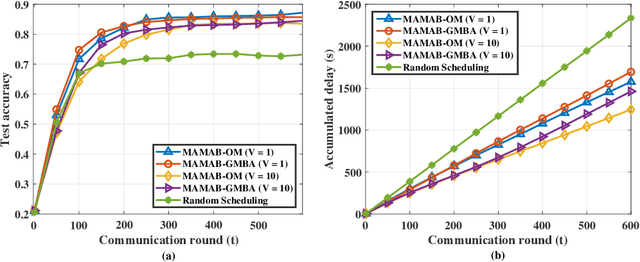
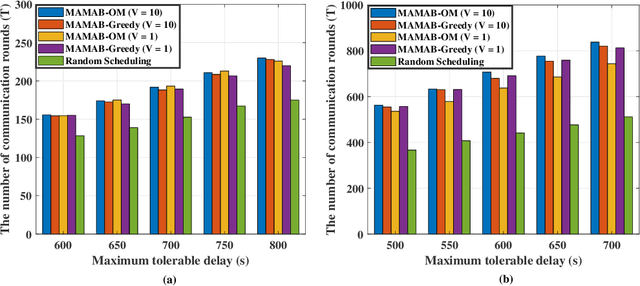
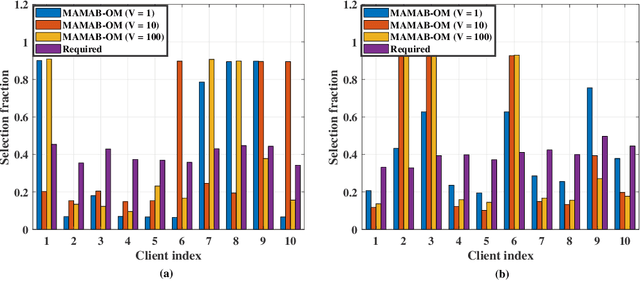
In federated learning (FL), model training is distributed over clients and local models are aggregated by a central server. The performance of uploaded models in such situations can vary widely due to imbalanced data distributions, potential demands on privacy protections, and quality of transmissions. In this paper, we aim to minimize FL training delay over wireless channels, constrained by overall training performance as well as each client's differential privacy (DP) requirement. We solve this problem in the framework of multi-agent multi-armed bandit (MAMAB) to deal with the situation where there are multiple clients confornting different unknown transmission environments, e.g., channel fading and interferences. Specifically, we first transform the long-term constraints on both training performance and each client's DP into a virtual queue based on the Lyapunov drift technique. Then, we convert the MAMAB to a max-min bipartite matching problem at each communication round, by estimating rewards with the upper confidence bound (UCB) approach. More importantly, we propose two efficient solutions to this matching problem, i.e., modified Hungarian algorithm and greedy matching with a better alternative (GMBA), in which the first one can achieve the optimal solution with a high complexity while the second one approaches a better trade-off by enabling a verified low-complexity with little performance loss. In addition, we develop an upper bound on the expected regret of this MAMAB based FL framework, which shows a linear growth over the logarithm of communication rounds, justifying its theoretical feasibility. Extensive experimental results are conducted to validate the effectiveness of our proposed algorithms, and the impacts of various parameters on the FL performance over wireless edge networks are also discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge