Local Saddle Point Optimization: A Curvature Exploitation Approach

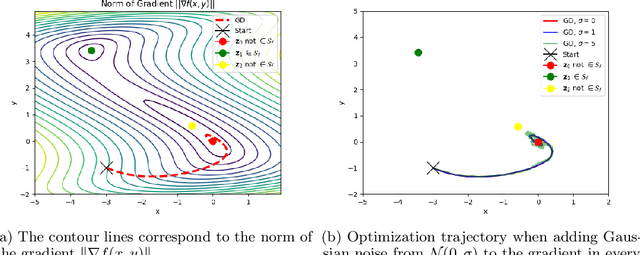
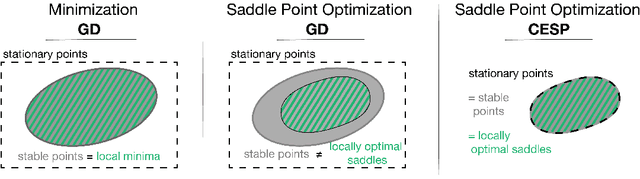
Gradient-based optimization methods are the most popular choice for finding local optima for classical minimization and saddle point problems. Here, we highlight a systemic issue of gradient dynamics that arise for saddle point problems, namely the presence of undesired stable stationary points that are no local optima. We propose a novel optimization approach that exploits curvature information in order to escape from these undesired stationary points. We prove that different optimization methods, including gradient method and adagrad, equipped with curvature exploitation can escape non-optimal stationary points. We also provide empirical results on common saddle point problems which confirm the advantage of using curvature exploitation.