Learning with Average Top-k Loss
Paper and Code
Dec 20, 2017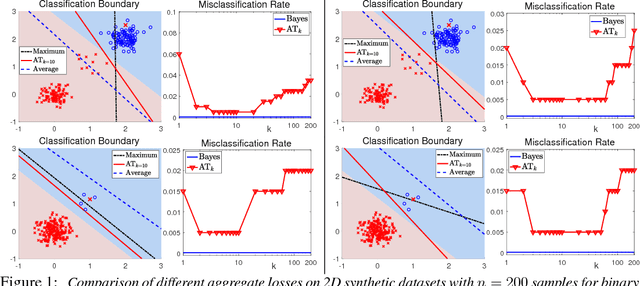
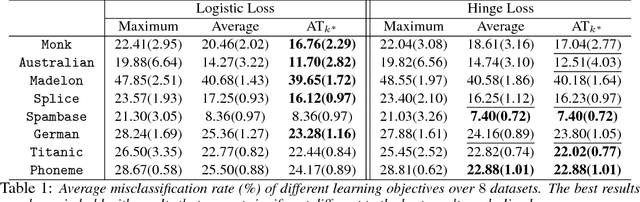
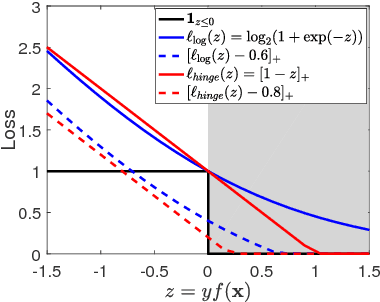
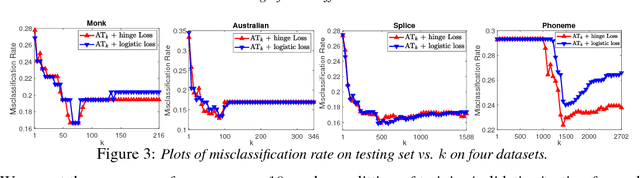
In this work, we introduce the {\em average top-$k$} (\atk) loss as a new aggregate loss for supervised learning, which is the average over the $k$ largest individual losses over a training dataset. We show that the \atk loss is a natural generalization of the two widely used aggregate losses, namely the average loss and the maximum loss, but can combine their advantages and mitigate their drawbacks to better adapt to different data distributions. Furthermore, it remains a convex function over all individual losses, which can lead to convex optimization problems that can be solved effectively with conventional gradient-based methods. We provide an intuitive interpretation of the \atk loss based on its equivalent effect on the continuous individual loss functions, suggesting that it can reduce the penalty on correctly classified data. We further give a learning theory analysis of \matk learning on the classification calibration of the \atk loss and the error bounds of \atk-SVM. We demonstrate the applicability of minimum average top-$k$ learning for binary classification and regression using synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge