Learning strides in convolutional neural networks
Paper and Code
Feb 03, 2022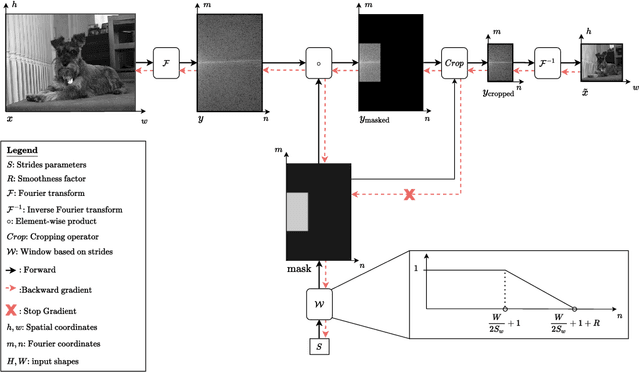
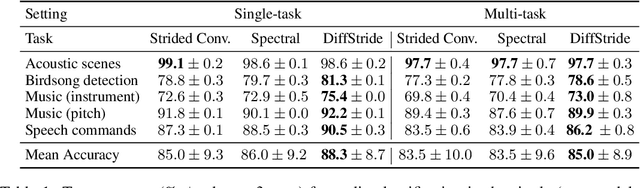
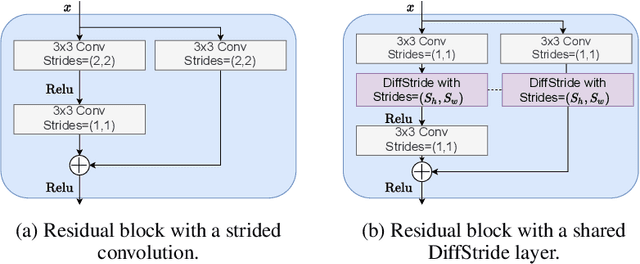
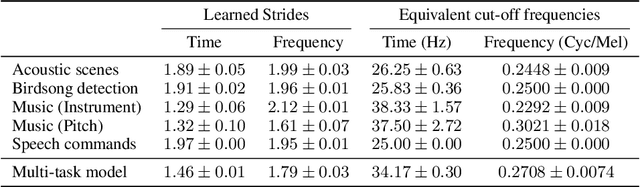
Convolutional neural networks typically contain several downsampling operators, such as strided convolutions or pooling layers, that progressively reduce the resolution of intermediate representations. This provides some shift-invariance while reducing the computational complexity of the whole architecture. A critical hyperparameter of such layers is their stride: the integer factor of downsampling. As strides are not differentiable, finding the best configuration either requires cross-validation or discrete optimization (e.g. architecture search), which rapidly become prohibitive as the search space grows exponentially with the number of downsampling layers. Hence, exploring this search space by gradient descent would allow finding better configurations at a lower computational cost. This work introduces DiffStride, the first downsampling layer with learnable strides. Our layer learns the size of a cropping mask in the Fourier domain, that effectively performs resizing in a differentiable way. Experiments on audio and image classification show the generality and effectiveness of our solution: we use DiffStride as a drop-in replacement to standard downsampling layers and outperform them. In particular, we show that introducing our layer into a ResNet-18 architecture allows keeping consistent high performance on CIFAR10, CIFAR100 and ImageNet even when training starts from poor random stride configurations. Moreover, formulating strides as learnable variables allows us to introduce a regularization term that controls the computational complexity of the architecture. We show how this regularization allows trading off accuracy for efficiency on ImageNet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge