Learning Stages: Phenomenon, Root Cause, Mechanism Hypothesis, and Implications

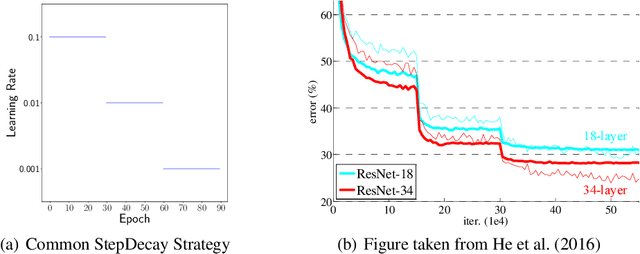
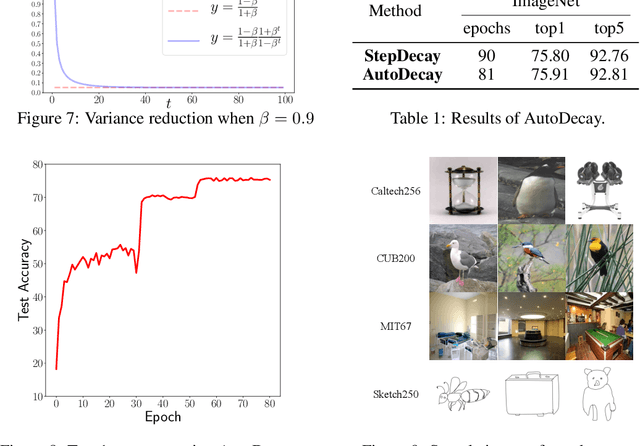
Under StepDecay learning rate strategy (decaying the learning rate after pre-defined epochs), it is a common phenomenon that the trajectories of learning statistics (training loss, test loss, test accuracy, etc.) are divided into several stages by sharp transitions. This paper studies the phenomenon in detail. Carefully designed experiments suggest the root cause to be the stochasticity of SGD. The convincing fact is the phenomenon disappears when Batch Gradient Descend is adopted. We then propose a hypothesis about the mechanism behind the phenomenon: the noise from SGD can be magnified to several levels by different learning rates, and only certain patterns are learnable within a certain level of noise. Patterns that can be learned under large noise are called easy patterns and patterns only learnable under small noise are called complex patterns. We derive several implications inspired by the hypothesis: (1) Since some patterns are not learnable until the next stage, we can design an algorithm to automatically detect the end of the current stage and switch to the next stage to expedite the training. The algorithm we design (called AutoDecay) shortens the time for training ResNet50 on ImageNet by $ 10 $\% without hurting the performance. (2) Since patterns are learned with increasing complexity, it is possible they have decreasing transferability. We study the transferability of models learned in different stages. Although later stage models have superior performance on ImageNet, we do find that they are less transferable. The verification of these two implications supports the hypothesis about the mechanism.