Learning Size and Shape of Calabi-Yau Spaces
Paper and Code
Nov 02, 2021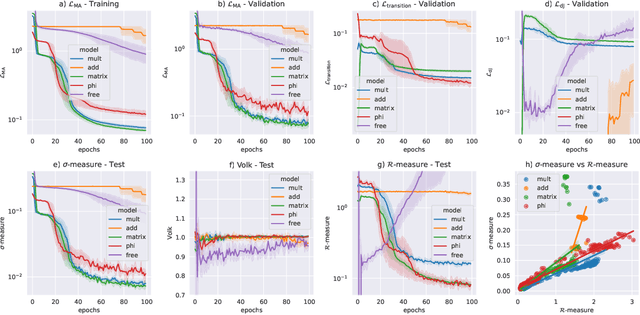
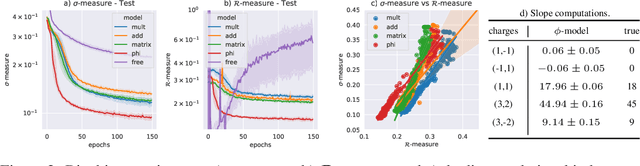
We present a new machine learning library for computing metrics of string compactification spaces. We benchmark the performance on Monte-Carlo sampled integrals against previous numerical approximations and find that our neural networks are more sample- and computation-efficient. We are the first to provide the possibility to compute these metrics for arbitrary, user-specified shape and size parameters of the compact space and observe a linear relation between optimization of the partial differential equation we are training against and vanishing Ricci curvature.
* 5 pages, 2 figures, to appear in: NeurIPS 2021 - ML4PS
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge