Learning Self-Expression Metrics for Scalable and Inductive Subspace Clustering
Paper and Code
Sep 27, 2020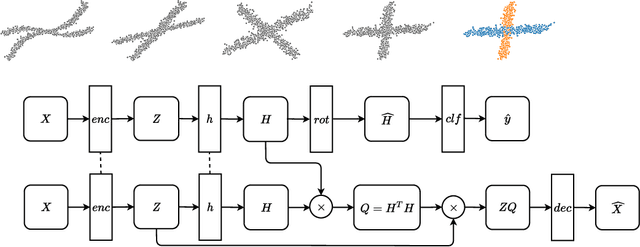

Subspace clustering has established itself as a state-of-the-art approach to clustering high-dimensional data. In particular, methods relying on the self-expressiveness property have recently proved especially successful. However, they suffer from two major shortcomings: First, a quadratic-size coefficient matrix is learned directly, preventing these methods from scaling beyond small datasets. Secondly, the trained models are transductive and thus cannot be used to cluster out-of-sample data unseen during training. Instead of learning self-expression coefficients directly, we propose a novel metric learning approach to learn instead a subspace affinity function using a siamese neural network architecture. Consequently, our model benefits from a constant number of parameters and a constant-size memory footprint, allowing it to scale to considerably larger datasets. In addition, we can formally show that out model is still able to exactly recover subspace clusters given an independence assumption. The siamese architecture in combination with a novel geometric classifier further makes our model inductive, allowing it to cluster out-of-sample data. Additionally, non-linear clusters can be detected by simply adding an auto-encoder module to the architecture. The whole model can then be trained end-to-end in a self-supervised manner. This work in progress reports promising preliminary results on the MNIST dataset. In the spirit of reproducible research, me make all code publicly available. In future work we plan to investigate several extensions of our model and to expand experimental evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge