Learning Relational Representations with Auto-encoding Logic Programs
Paper and Code
Mar 29, 2019


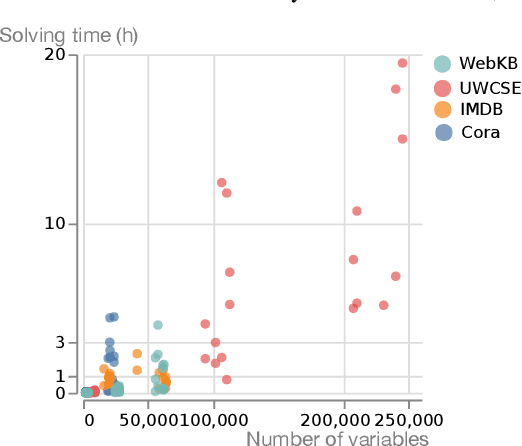
Deep learning methods capable of handling relational data have proliferated over the last years. In contrast to traditional relational learning methods that leverage first-order logic for representing such data, these deep learning methods aim at re-representing symbolic relational data in Euclidean spaces. They offer better scalability, but can only numerically approximate relational structures and are less flexible in terms of reasoning tasks supported. This paper introduces a novel framework for relational representation learning that combines the best of both worlds. This framework, inspired by the auto-encoding principle, uses first-order logic as a data representation language, and the mapping between the original and latent representation is done by means of logic programs instead of neural networks. We show how learning can be cast as a constraint optimisation problem for which existing solvers can be used. The use of logic as a representation language makes the proposed framework more accurate (as the representation is exact, rather than approximate), more flexible, and more interpretable than deep learning methods. We experimentally show that these latent representations are indeed beneficial in relational learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge