Learning Privately over Distributed Features: An ADMM Sharing Approach
Paper and Code
Jul 17, 2019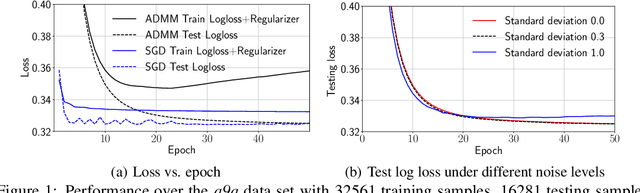
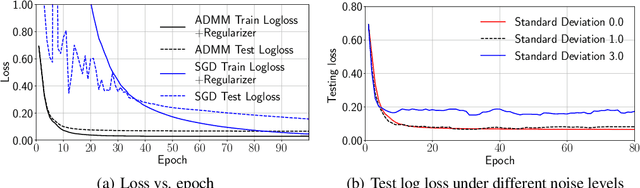
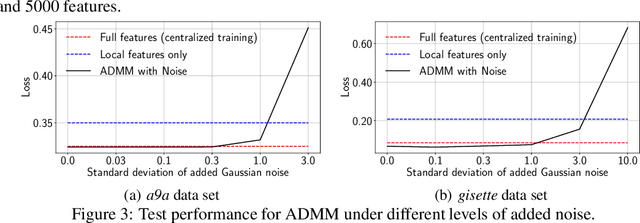
Distributed machine learning has been widely studied in order to handle exploding amount of data. In this paper, we study an important yet less visited distributed learning problem where features are inherently distributed or vertically partitioned among multiple parties, and sharing of raw data or model parameters among parties is prohibited due to privacy concerns. We propose an ADMM sharing framework to approach risk minimization over distributed features, where each party only needs to share a single value for each sample in the training process, thus minimizing the data leakage risk. We establish convergence and iteration complexity results for the proposed parallel ADMM algorithm under non-convex loss. We further introduce a novel differentially private ADMM sharing algorithm and bound the privacy guarantee with carefully designed noise perturbation. The experiments based on a prototype system shows that the proposed ADMM algorithms converge efficiently in a robust fashion, demonstrating advantage over gradient based methods especially for data set with high dimensional feature spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge