Learning Invariant Representations using Inverse Contrastive Loss
Paper and Code
Feb 16, 2021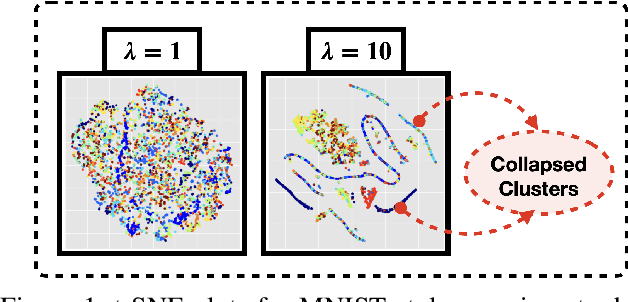
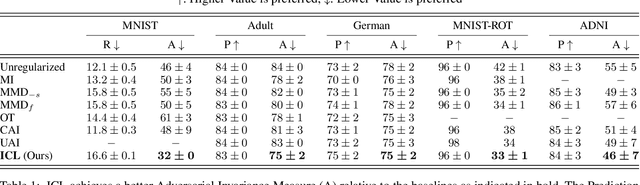
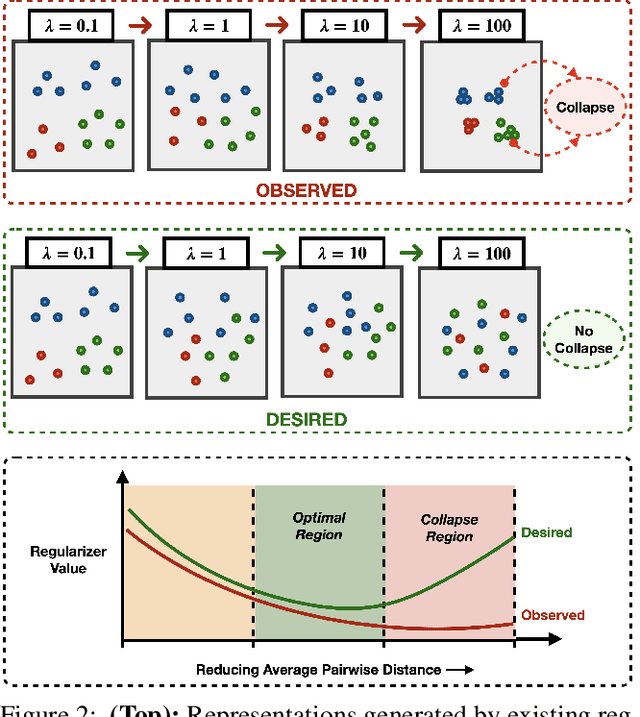
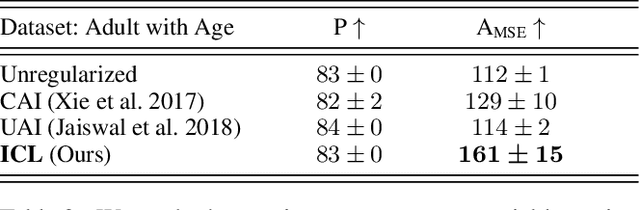
Learning invariant representations is a critical first step in a number of machine learning tasks. A common approach corresponds to the so-called information bottleneck principle in which an application dependent function of mutual information is carefully chosen and optimized. Unfortunately, in practice, these functions are not suitable for optimization purposes since these losses are agnostic of the metric structure of the parameters of the model. We introduce a class of losses for learning representations that are invariant to some extraneous variable of interest by inverting the class of contrastive losses, i.e., inverse contrastive loss (ICL). We show that if the extraneous variable is binary, then optimizing ICL is equivalent to optimizing a regularized MMD divergence. More generally, we also show that if we are provided a metric on the sample space, our formulation of ICL can be decomposed into a sum of convex functions of the given distance metric. Our experimental results indicate that models obtained by optimizing ICL achieve significantly better invariance to the extraneous variable for a fixed desired level of accuracy. In a variety of experimental settings, we show applicability of ICL for learning invariant representations for both continuous and discrete extraneous variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge