Learning Energy-based Model with Flow-based Backbone by Neural Transport MCMC

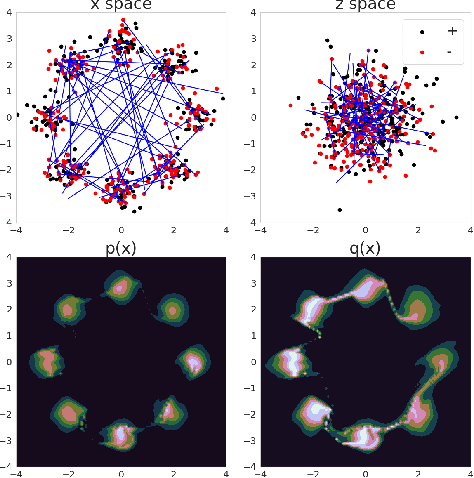
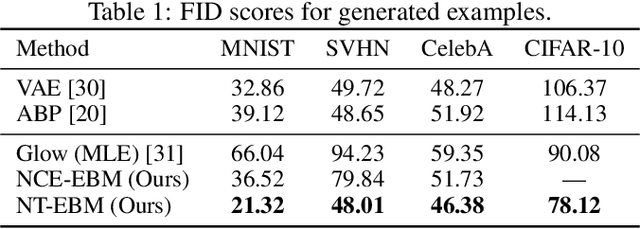
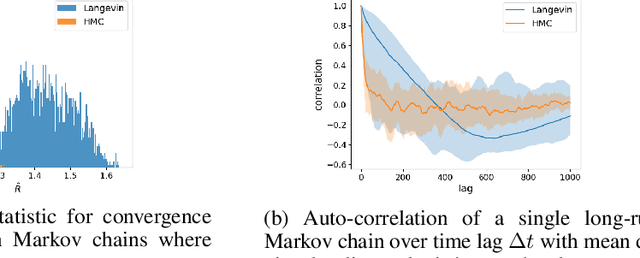
Learning energy-based model (EBM) requires MCMC sampling of the learned model as the inner loop of the learning algorithm. However, MCMC sampling of EBM in data space is generally not mixing, because the energy function, which is usually parametrized by deep network, is highly multi-modal in the data space. This is a serious handicap for both the theory and practice of EBM. In this paper, we propose to learn EBM with a flow-based model serving as a backbone, so that the EBM is a correction or an exponential tilting of the flow-based model. We show that the model has a particularly simple form in the space of the latent variables of the flow-based model, and MCMC sampling of the EBM in the latent space, which is a simple special case of neural transport MCMC, mixes well and traverses modes in the data space. This enables proper sampling and learning of EBM.