Learning Empirical Bregman Divergence for Uncertain Distance Representation
Paper and Code
Apr 18, 2023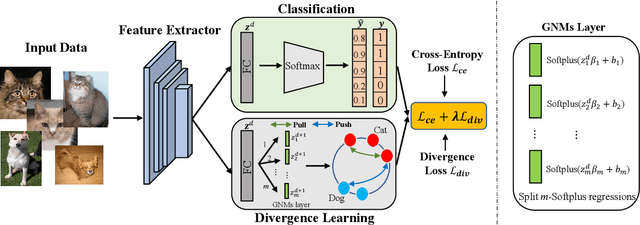
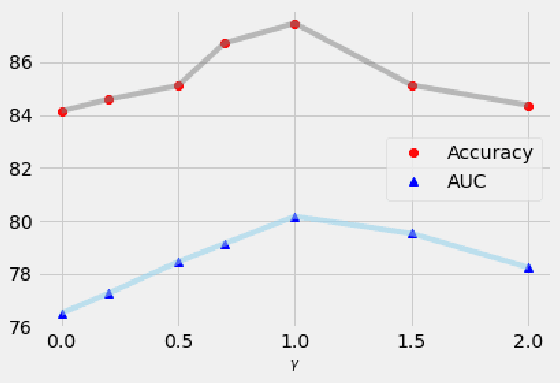
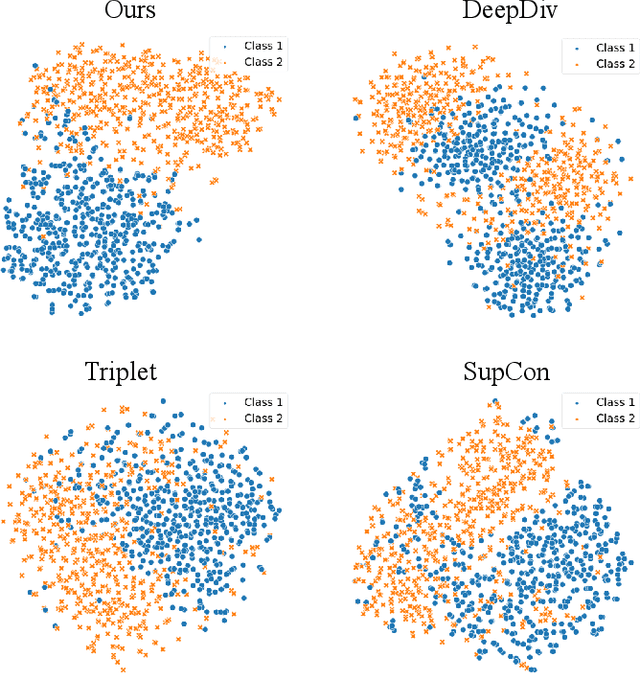

Deep metric learning techniques have been used for visual representation in various supervised and unsupervised learning tasks through learning embeddings of samples with deep networks. However, classic approaches, which employ a fixed distance metric as a similarity function between two embeddings, may lead to suboptimal performance for capturing the complex data distribution. The Bregman divergence generalizes measures of various distance metrics and arises throughout many fields of deep metric learning. In this paper, we first show how deep metric learning loss can arise from the Bregman divergence. We then introduce a novel method for learning empirical Bregman divergence directly from data based on parameterizing the convex function underlying the Bregman divergence with a deep learning setting. We further experimentally show that our approach performs effectively on five popular public datasets compared to other SOTA deep metric learning methods, particularly for pattern recognition problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge