Learning Deep Neural Policies with Stability Guarantees

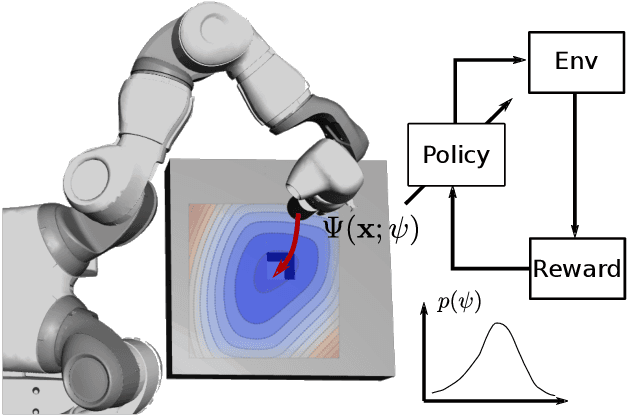
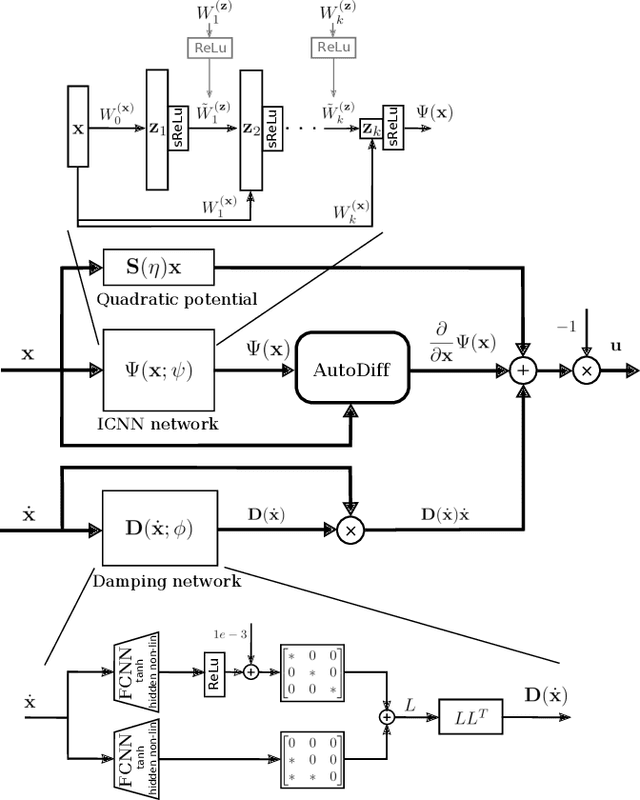
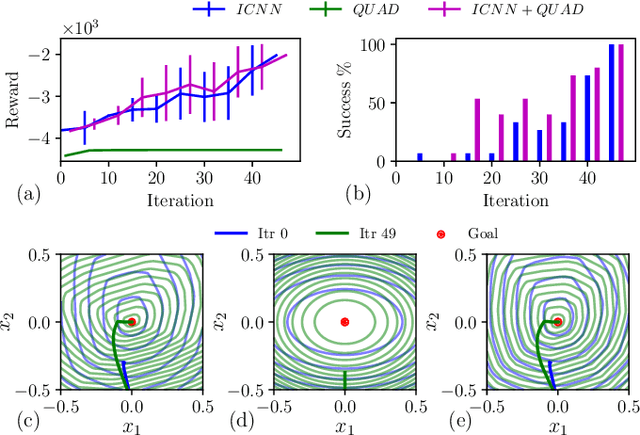
Reinforcement learning (RL) has been successfully used to solve various robotic control tasks. However, most of the existing works do not address the issue of control stability. This is in sharp contrast to the control theory community where the well-established norm is to prove stability whenever a control law is synthesized. What makes guaranteeing stability during RL difficult is threefold: non interpretable neural network policies, unknown system dynamics and random exploration. We contribute towards solving the stable RL problem in the context of robotic manipulation that may involve physical contact with the environment. Our solution is derived from physics-based prior that originates from Lagrangian mechanics and does not involve learning any dynamics model. We show how to parameterize the resulting $\textit{energy shaping}$ policy as a deep neural network that consists of a convex potential function and a velocity dependent damping component. Our experiments, that include a real-world peg insertion task by a 7-DOF robot, validate the proposed policy structure and demonstrate the benefits of stability in RL.