Learning Decision Trees with Gradient Descent
Paper and Code
May 05, 2023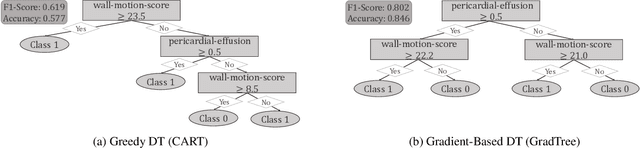

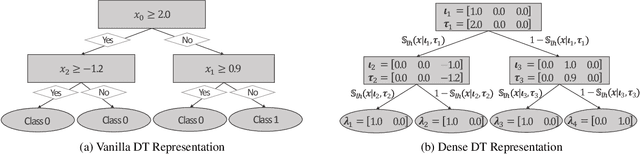
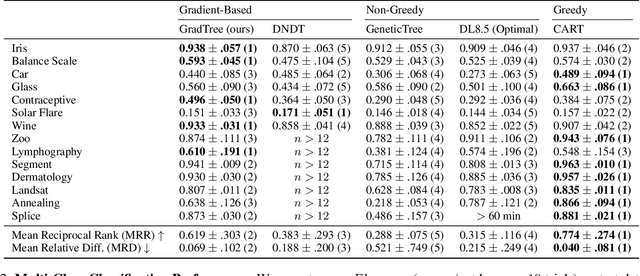
Decision Trees (DTs) are commonly used for many machine learning tasks due to their high degree of interpretability. However, learning a DT from data is a difficult optimization problem, as it is non-convex and non-differentiable. Therefore, common approaches learn DTs using a greedy growth algorithm that minimizes the impurity locally at each internal node. Unfortunately, this greedy procedure can lead to suboptimal trees. In this paper, we present a novel approach for learning hard, axis-aligned DTs with gradient descent. The proposed method uses backpropagation with a straight-through operator on a dense DT representation to jointly optimize all tree parameters. Our approach outperforms existing methods on binary classification benchmarks and achieves competitive results for multi-class tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge