Learning Credible Models
Paper and Code
Jun 07, 2018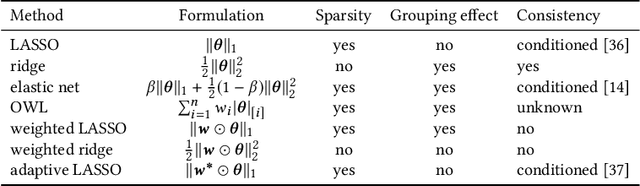
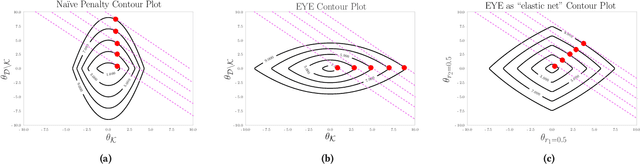
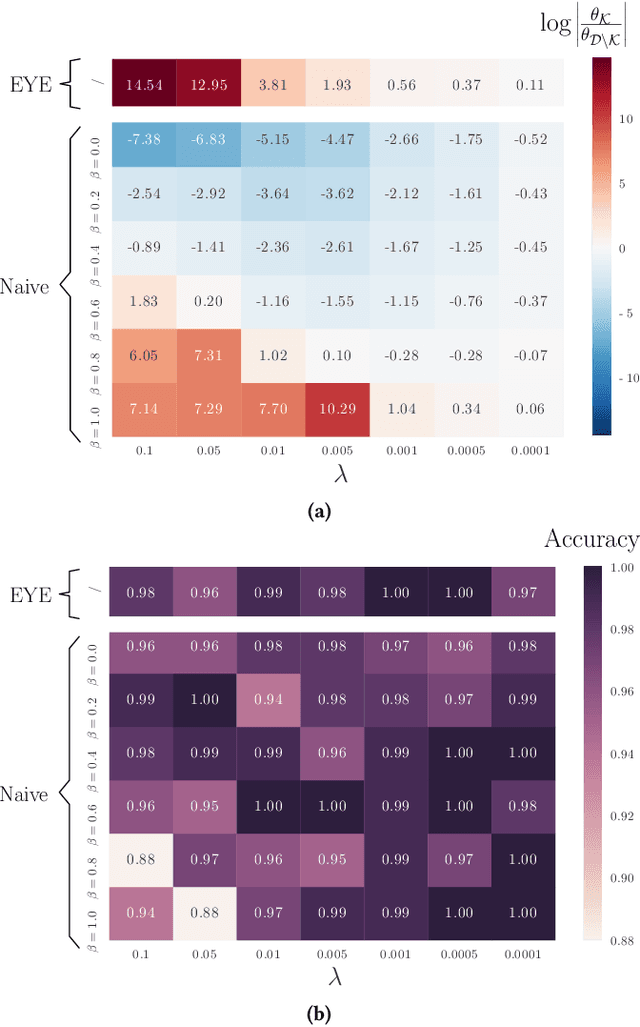
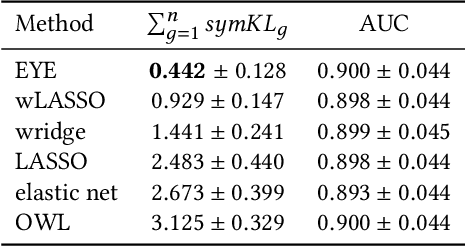
In many settings, it is important that a model be capable of providing reasons for its predictions (i.e., the model must be interpretable). However, the model's reasoning may not conform with well-established knowledge. In such cases, while interpretable, the model lacks \textit{credibility}. In this work, we formally define credibility in the linear setting and focus on techniques for learning models that are both accurate and credible. In particular, we propose a regularization penalty, expert yielded estimates (EYE), that incorporates expert knowledge about well-known relationships among covariates and the outcome of interest. We give both theoretical and empirical results comparing our proposed method to several other regularization techniques. Across a range of settings, experiments on both synthetic and real data show that models learned using the EYE penalty are significantly more credible than those learned using other penalties. Applied to a large-scale patient risk stratification task, our proposed technique results in a model whose top features overlap significantly with known clinical risk factors, while still achieving good predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge