Learning beyond Predefined Label Space via Bayesian Nonparametric Topic Modelling
Paper and Code
Oct 10, 2019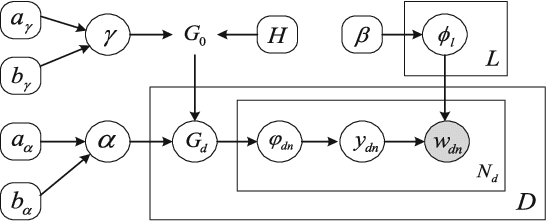

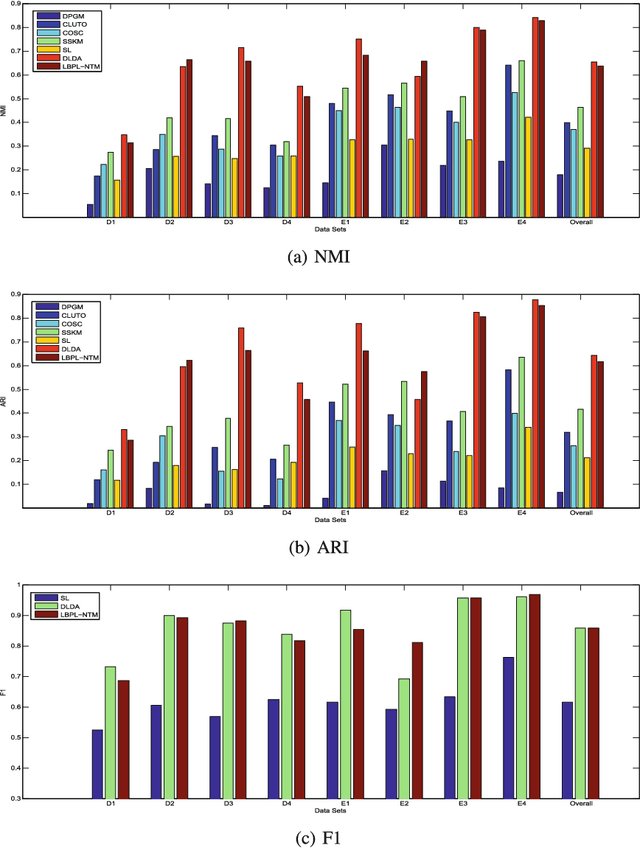
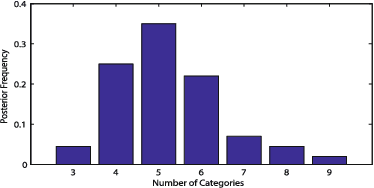
In real world machine learning applications, testing data may contain some meaningful new categories that have not been seen in labeled training data. To simultaneously recognize new data categories and assign most appropriate category labels to the data actually from known categories, existing models assume the number of unknown new categories is pre-specified, though it is difficult to determine in advance. In this paper, we propose a Bayesian nonparametric topic model to automatically infer this number, based on the hierarchical Dirichlet process and the notion of latent Dirichlet allocation. Exact inference in our model is intractable, so we provide an efficient collapsed Gibbs sampling algorithm for approximate posterior inference. Extensive experiments on various text data sets show that: (a) compared with parametric approaches that use pre-specified true number of new categories, the proposed nonparametric approach can yield comparable performance; and (b) when the exact number of new categories is unavailable, i.e. the parametric approaches only have a rough idea about the new categories, our approach has evident performance advantages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge