Latent Variable Modelling with Hyperbolic Normalizing Flows
Paper and Code
Feb 18, 2020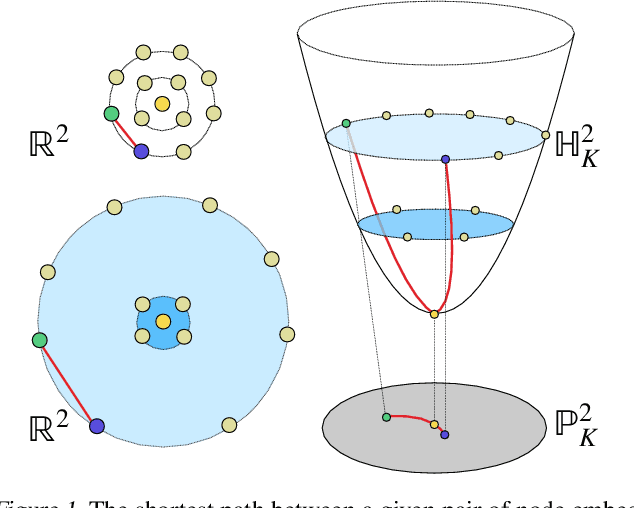
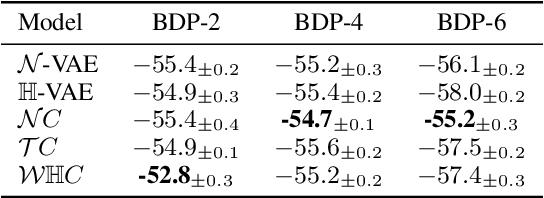
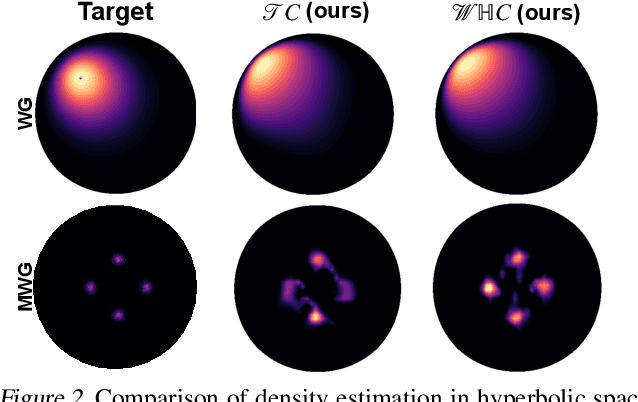

The choice of approximate posterior distributions plays a central role in stochastic variational inference (SVI). One effective solution is the use of normalizing flows \cut{defined on Euclidean spaces} to construct flexible posterior distributions. However, one key limitation of existing normalizing flows is that they are restricted to the Euclidean space and are ill-equipped to model data with an underlying hierarchical structure. To address this fundamental limitation, we present the first extension of normalizing flows to hyperbolic spaces. We first elevate normalizing flows to hyperbolic spaces using coupling transforms defined on the tangent bundle, termed Tangent Coupling ($\mathcal{TC}$). We further introduce Wrapped Hyperboloid Coupling ($\mathcal{W}\mathbb{H}C$), a fully invertible and learnable transformation that explicitly utilizes the geometric structure of hyperbolic spaces, allowing for expressive posteriors while being efficient to sample from. We demonstrate the efficacy of our novel normalizing flow over hyperbolic VAEs and Euclidean normalizing flows. Our approach achieves improved performance on density estimation, as well as reconstruction of real-world graph data, which exhibit a hierarchical structure. Finally, we show that our approach can be used to power a generative model over hierarchical data using hyperbolic latent variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge