Latent Optimal Paths by Gumbel Propagation for Variational Bayesian Dynamic Programming
Paper and Code
Jun 05, 2023
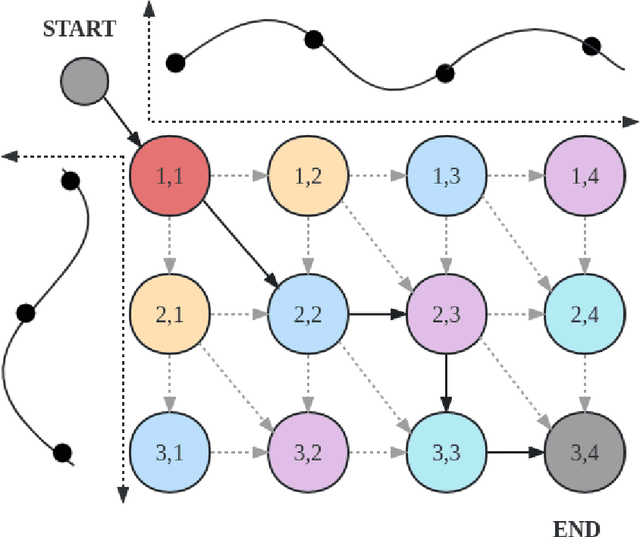


We propose a unified approach to obtain structured sparse optimal paths in the latent space of a variational autoencoder (VAE) using dynamic programming and Gumbel propagation. We solve the classical optimal path problem by a probability softening solution, called the stochastic optimal path, and transform a wide range of DP problems into directed acyclic graphs in which all possible paths follow a Gibbs distribution. We show the equivalence of the Gibbs distribution to a message-passing algorithm by the properties of the Gumbel distribution and give all the ingredients required for variational Bayesian inference. Our approach obtaining latent optimal paths enables end-to-end training for generative tasks in which models rely on the information of unobserved structural features. We validate the behavior of our approach and showcase its applicability in two real-world applications: text-to-speech and singing voice synthesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge