Koopman Q-learning: Offline Reinforcement Learning via Symmetries of Dynamics

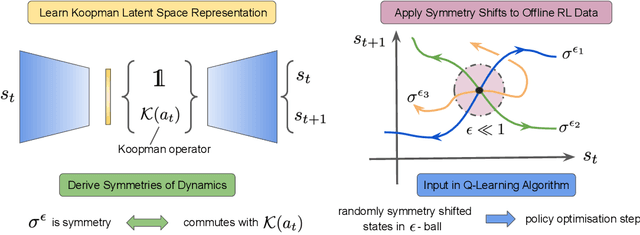
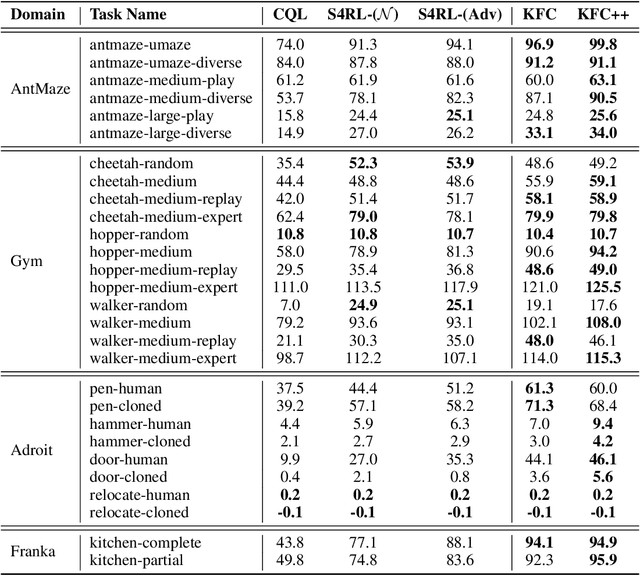
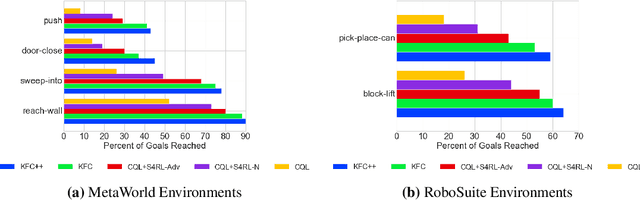
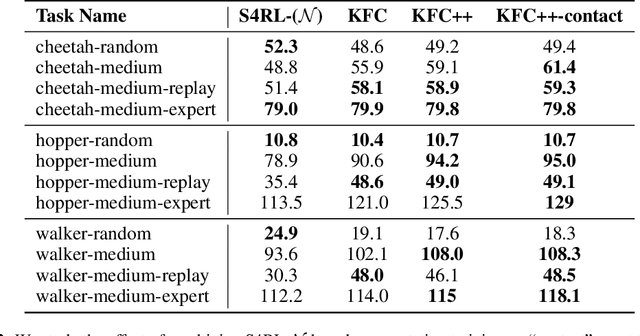
Offline reinforcement learning leverages large datasets to train policies without interactions with the environment. The learned policies may then be deployed in real-world settings where interactions are costly or dangerous. Current algorithms over-fit to the training dataset and as a consequence perform poorly when deployed to out-of-distribution generalizations of the environment. We aim to address these limitations by learning a Koopman latent representation which allows us to infer symmetries of the system's underlying dynamic. The latter is then utilized to extend the otherwise static offline dataset during training; this constitutes a novel data augmentation framework which reflects the system's dynamic and is thus to be interpreted as an exploration of the environments phase space. To obtain the symmetries we employ Koopman theory in which nonlinear dynamics are represented in terms of a linear operator acting on the space of measurement functions of the system and thus symmetries of the dynamics may be inferred directly. We provide novel theoretical results on the existence and nature of symmetries relevant for control systems such as reinforcement learning settings. Moreover, we empirically evaluate our method on several benchmark offline reinforcement learning tasks and datasets including D4RL, Metaworld and Robosuite and find that by using our framework we consistently improve the state-of-the-art for Q-learning methods.