Koopman Neural Forecaster for Time Series with Temporal Distribution Shifts

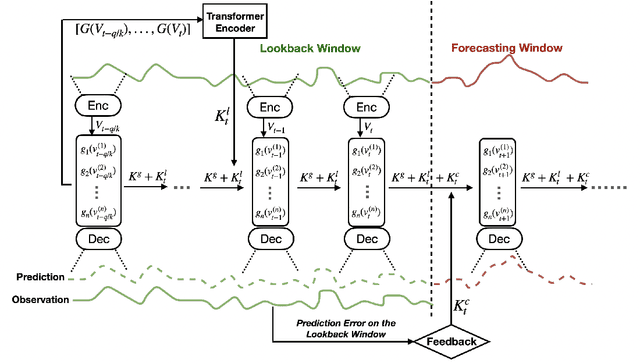
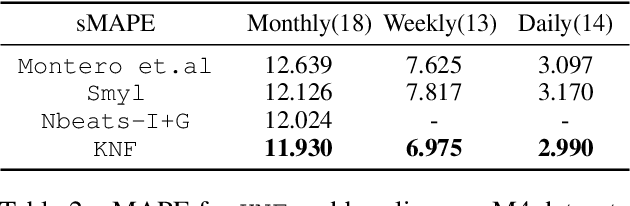
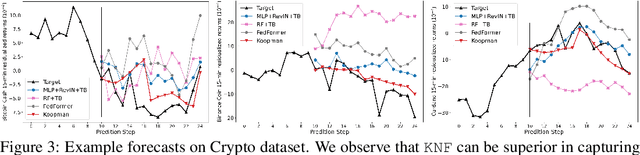
Temporal distributional shifts, with underlying dynamics changing over time, frequently occur in real-world time series, and pose a fundamental challenge for deep neural networks (DNNs). In this paper, we propose a novel deep sequence model based on the Koopman theory for time series forecasting: Koopman Neural Forecaster (KNF) that leverages DNNs to learn the linear Koopman space and the coefficients of chosen measurement functions. KNF imposes appropriate inductive biases for improved robustness against distributional shifts, employing both a global operator to learn shared characteristics, and a local operator to capture changing dynamics, as well as a specially-designed feedback loop to continuously update the learnt operators over time for rapidly varying behaviors. To the best of our knowledge, this is the first time that Koopman theory is applied to real-world chaotic time series without known governing laws. We demonstrate that KNF achieves the superior performance compared to the alternatives, on multiple time series datasets that are shown to suffer from distribution shifts.