Kernel-based Diffusion Approximated Markov Decision Processes for Off-Road Autonomous Navigation and Control

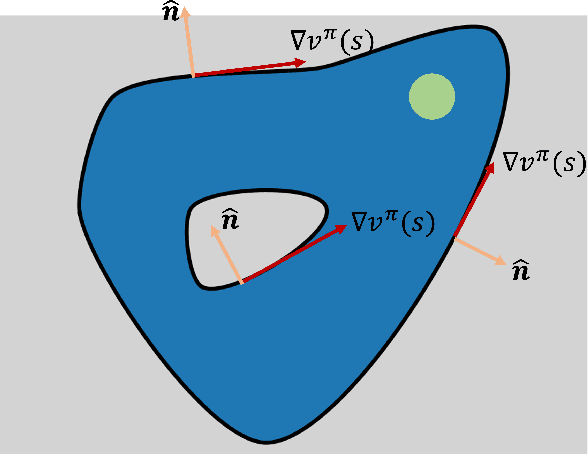
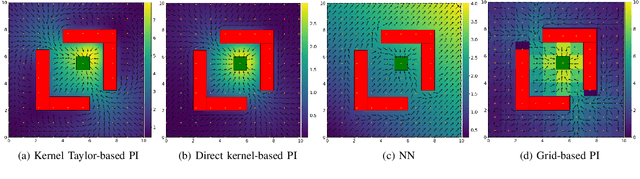
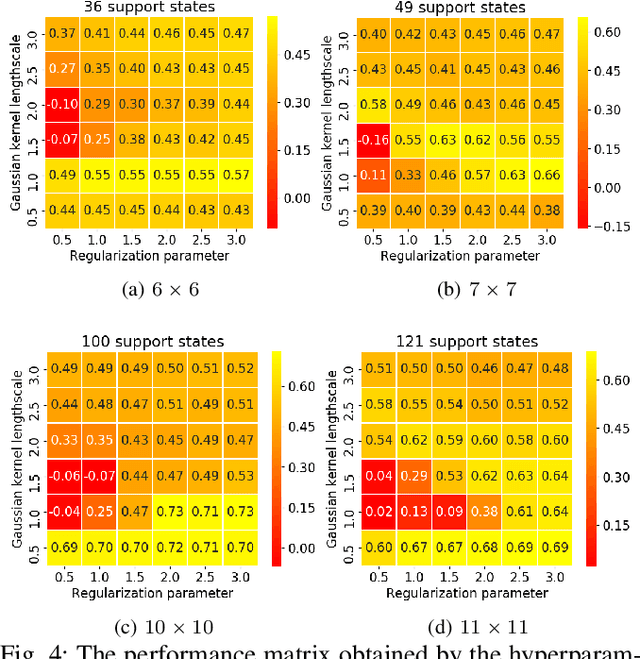
We propose a diffusion approximation method to the continuous-state Markov Decision Processes (MDPs) that can be utilized to address autonomous navigation and control in unstructured off-road environments. In contrast to most decision-theoretic planning frameworks that assume fully known state transition models, we design a method that eliminates such a strong assumption that is often extremely difficult to engineer in reality. We first take the second-order Taylor expansion of the value function. The Bellman optimality equation is then approximated by a partial differential equation, which only relies on the first and second moments of the transition model. By combining the kernel representation of the value function, we then design an efficient policy iteration algorithm whose policy evaluation step can be represented as a linear system of equations characterized by a finite set of supporting states. We first validate the proposed method through extensive simulations in $2D$ obstacle avoidance and $2.5D$ terrain navigation problems. The results show that the proposed approach leads to a much superior performance over several baselines. We then develop a system that integrates our decision-making framework with onboard perception and conduct real-world experiments in both cluttered indoor and unstructured outdoor environments. The results from the physical systems further demonstrate the applicability of our method in challenging real-world environments.