Keep Guessing? When Considering Inference Scaling, Mind the Baselines
Paper and Code
Oct 20, 2024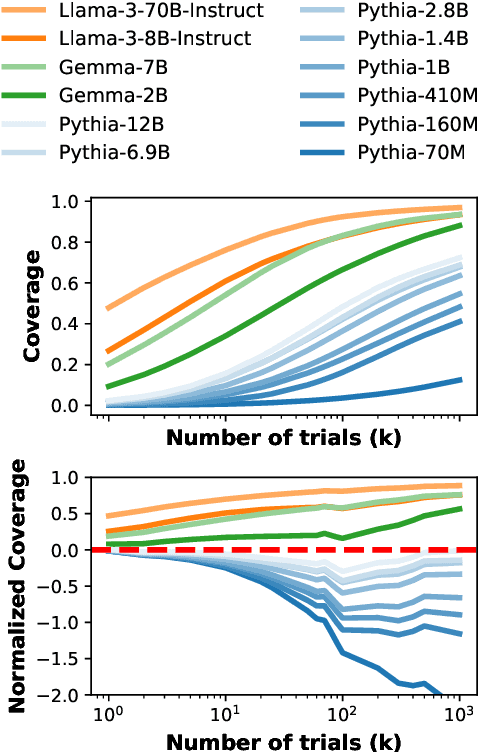
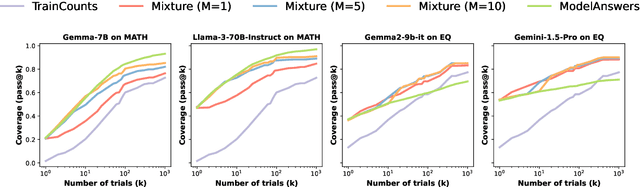

Scaling inference compute in large language models (LLMs) through repeated sampling consistently increases the coverage (fraction of problems solved) as the number of samples increases. We conjecture that this observed improvement is partially due to the answer distribution of standard evaluation benchmarks, which is skewed towards a relatively small set of common answers. To test this conjecture, we define a baseline that enumerates answers according to their prevalence in the training set. Experiments spanning two domains -- mathematical reasoning and factual knowledge -- reveal that this baseline outperforms repeated model sampling for some LLMs, while the coverage for others is on par with that of a mixture strategy that obtains $k$ answers by using only $10$ model samples and similarly guessing the remaining $k-10$ attempts via enumeration. Our baseline enables a more accurate measurement of how much repeated sampling improves coverage in such settings beyond prompt-agnostic guessing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge