ITENE: Intrinsic Transfer Entropy Neural Estimator
Paper and Code
Jan 08, 2020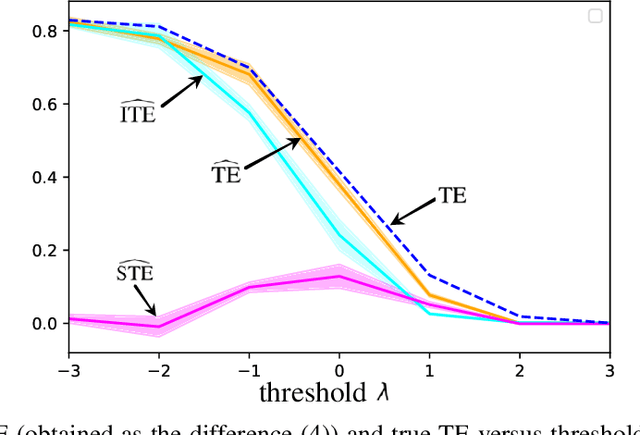
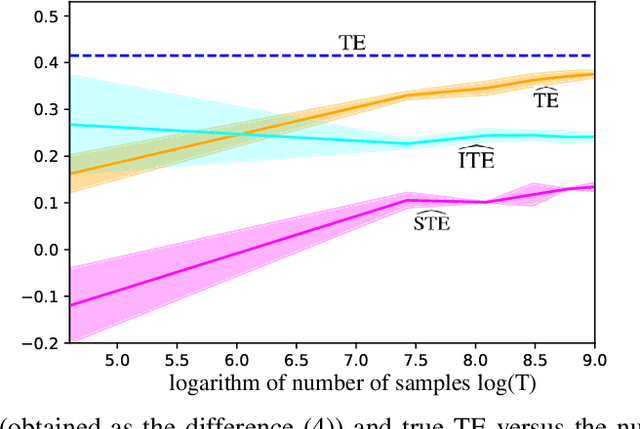
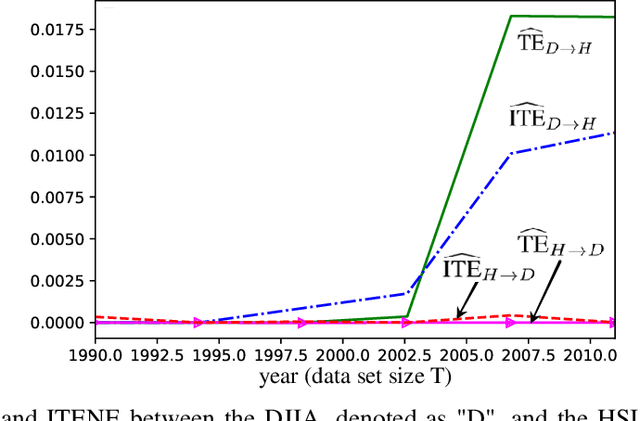
Quantifying the directionality of information flow is instrumental in understanding, and possibly controlling, the operation of many complex systems, such as transportation, social, neural, or gene-regulatory networks. The standard Transfer Entropy (TE) metric follows Granger's causality principle by measuring the Mutual Information (MI) between the past states of a source signal $X$ and the future state of a target signal $Y$ while conditioning on past states of $Y$. Hence, the TE quantifies the improvement, as measured by the log-loss, in the prediction of the target sequence $Y$ that can be accrued when, in addition to the past of $Y$, one also has available past samples from $X$. However, by conditioning on the past of $Y$, the TE also measures information that can be synergistically extracted by observing both the past of $X$ and $Y$, and not solely the past of $X$. Building on a private key agreement formulation, the Intrinsic TE (ITE) aims to discount such synergistic information to quantify the degree to which $X$ is \emph{individually} predictive of $Y$, independent of $Y$'s past. In this paper, an estimator of the ITE is proposed that is inspired by the recently proposed Mutual Information Neural Estimation (MINE). The estimator is based on variational bound on the KL divergence, two-sample neural network classifiers, and the pathwise estimator of Monte Carlo gradients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge