Inverse Reinforcement Learning with Explicit Policy Estimates
Paper and Code
Mar 04, 2021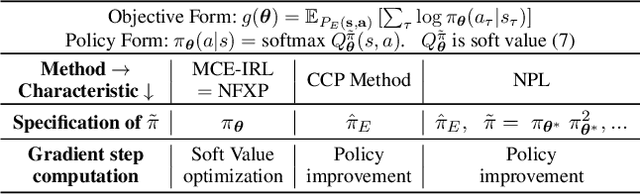


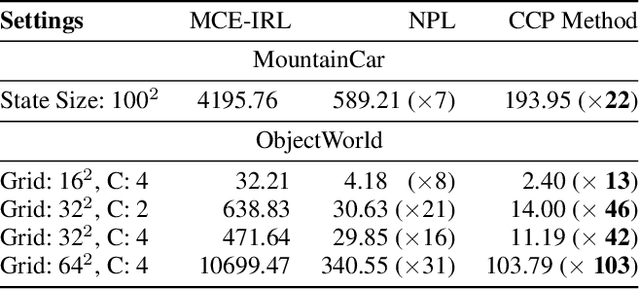
Various methods for solving the inverse reinforcement learning (IRL) problem have been developed independently in machine learning and economics. In particular, the method of Maximum Causal Entropy IRL is based on the perspective of entropy maximization, while related advances in the field of economics instead assume the existence of unobserved action shocks to explain expert behavior (Nested Fixed Point Algorithm, Conditional Choice Probability method, Nested Pseudo-Likelihood Algorithm). In this work, we make previously unknown connections between these related methods from both fields. We achieve this by showing that they all belong to a class of optimization problems, characterized by a common form of the objective, the associated policy and the objective gradient. We demonstrate key computational and algorithmic differences which arise between the methods due to an approximation of the optimal soft value function, and describe how this leads to more efficient algorithms. Using insights which emerge from our study of this class of optimization problems, we identify various problem scenarios and investigate each method's suitability for these problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge