Interdependency Matters: Graph Alignment for Multivariate Time Series Anomaly Detection
Paper and Code
Oct 11, 2024


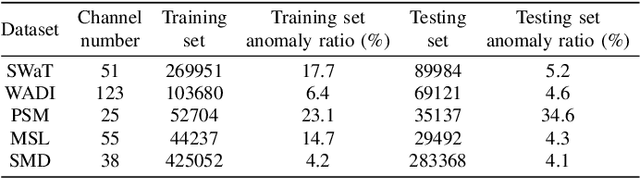
Anomaly detection in multivariate time series (MTS) is crucial for various applications in data mining and industry. Current industrial methods typically approach anomaly detection as an unsupervised learning task, aiming to identify deviations by estimating the normal distribution in noisy, label-free datasets. These methods increasingly incorporate interdependencies between channels through graph structures to enhance accuracy. However, the role of interdependencies is more critical than previously understood, as shifts in interdependencies between MTS channels from normal to anomalous data are significant. This observation suggests that \textit{anomalies could be detected by changes in these interdependency graph series}. To capitalize on this insight, we introduce MADGA (MTS Anomaly Detection via Graph Alignment), which redefines anomaly detection as a graph alignment (GA) problem that explicitly utilizes interdependencies for anomaly detection. MADGA dynamically transforms subsequences into graphs to capture the evolving interdependencies, and Graph alignment is performed between these graphs, optimizing an alignment plan that minimizes cost, effectively minimizing the distance for normal data and maximizing it for anomalous data. Uniquely, our GA approach involves explicit alignment of both nodes and edges, employing Wasserstein distance for nodes and Gromov-Wasserstein distance for edges. To our knowledge, this is the first application of GA to MTS anomaly detection that explicitly leverages interdependency for this purpose. Extensive experiments on diverse real-world datasets validate the effectiveness of MADGA, demonstrating its capability to detect anomalies and differentiate interdependencies, consistently achieving state-of-the-art across various scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge