Inferring Obstacles and Path Validity from Visibility-Constrained Demonstrations
Paper and Code
May 11, 2020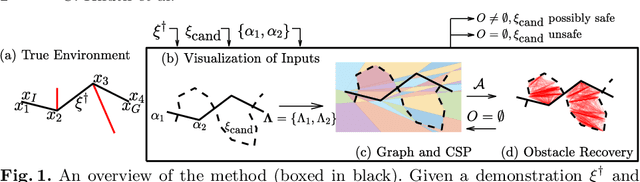
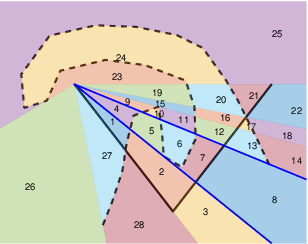
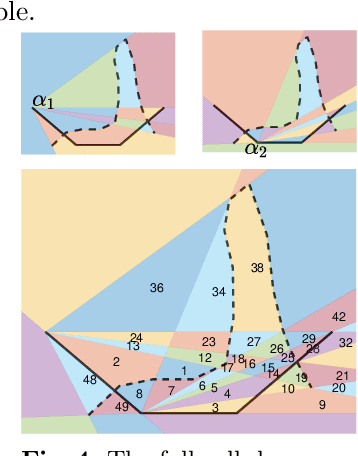
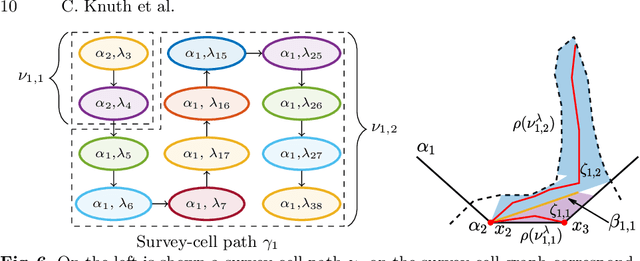
Many methods in learning from demonstration assume that the demonstrator has knowledge of the full environment. However, in many scenarios, a demonstrator only sees part of the environment and they continuously replan as they gather information. To plan new paths or to reconstruct the environment, we must consider the visibility constraints and replanning process of the demonstrator, which, to our knowledge, has not been done in previous work. We consider the problem of inferring obstacle configurations in a 2D environment from demonstrated paths for a point robot that is capable of seeing in any direction but not through obstacles. Given a set of \textit{survey points}, which describe where the demonstrator obtains new information, and a candidate path, we construct a Constraint Satisfaction Problem (CSP) on a cell decomposition of the environment. We parameterize a set of obstacles corresponding to an assignment from the CSP and sample from the set to find valid environments. We show that there is a probabilistically-complete, yet not entirely tractable, algorithm that can guarantee novel paths in the space are unsafe or possibly safe. We also present an incomplete, but empirically-successful, heuristic-guided algorithm that we apply in our experiments to 1) planning novel paths and 2) recovering a probabilistic representation of the environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge