Incentivizing Exploration with Unbiased Histories

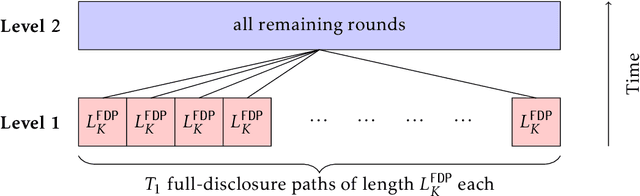
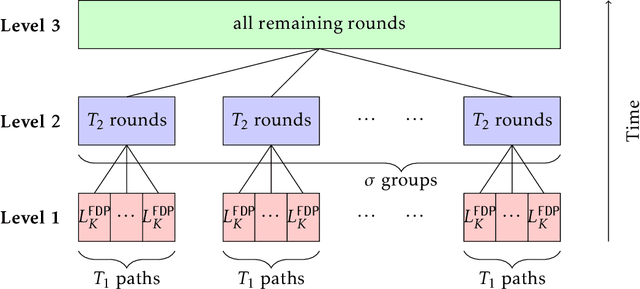
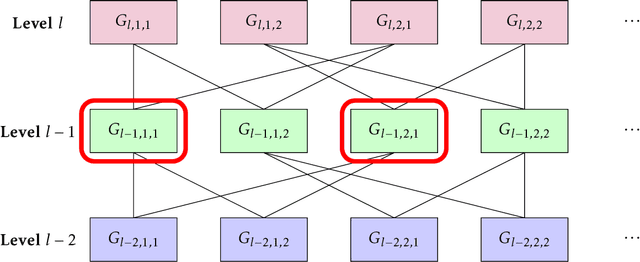
In a social learning setting, there is a set of actions, each of which has a payoff that depends on a hidden state of the world. A sequence of agents each chooses an action with the goal of maximizing payoff given estimates of the state of the world. A disclosure policy tries to coordinate the choices of the agents by sending messages about the history of past actions. The goal of the algorithm is to minimize the regret of the action sequence. In this paper, we study a particular class of disclosure policies that use messages, called unbiased subhistories, consisting of the actions and rewards from by a subsequence of past agents, where the subsequence is chosen ahead of time. One trivial message of this form contains the full history; a disclosure policy that chooses to use such messages risks inducing herding behavior among the agents and thus has regret linear in the number of rounds. Our main result is a disclosure policy using unbiased subhistories that obtains regret $\tilde{O}(\sqrt{T})$. We also exhibit simpler policies with higher, but still sublinear, regret. These policies can be interpreted as dividing a sublinear number of agents into constant-sized focus groups, whose histories are then fed to future agents.