Improved Surrogate Modeling of Fluid Dynamics with Physics-Informed Neural Networks
Paper and Code
May 05, 2021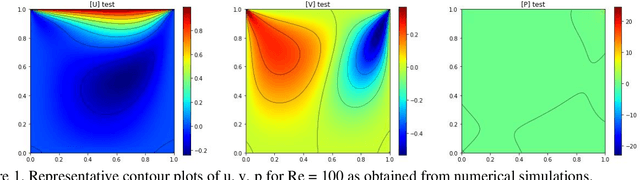
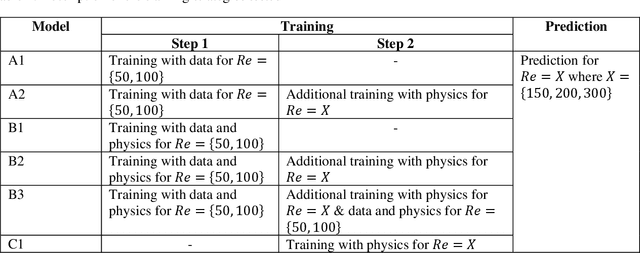
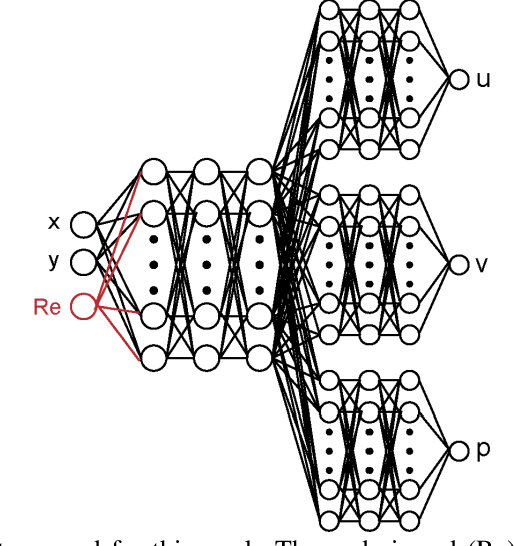
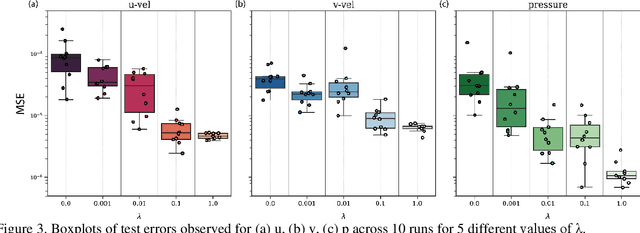
Physics-Informed Neural Networks (PINNs) have recently shown great promise as a way of incorporating physics-based domain knowledge, including fundamental governing equations, into neural network models for many complex engineering systems. They have been particularly effective in the area of inverse problems, where boundary conditions may be ill-defined, and data-absent scenarios, where typical supervised learning approaches will fail. Here, we further explore the use of this modeling methodology to surrogate modeling of a fluid dynamical system, and demonstrate additional undiscussed and interesting advantages of such a modeling methodology over conventional data-driven approaches: 1) improving the model's predictive performance even with incomplete description of the underlying physics; 2) improving the robustness of the model to noise in the dataset; 3) reduced effort to convergence during optimization for a new, previously unseen scenario by transfer optimization of a pre-existing model. Hence, we noticed the inclusion of a physics-based regularization term can substantially improve the equivalent data-driven surrogate model in many substantive ways, including an order of magnitude improvement in test error when the dataset is very noisy, and a 2-3x improvement when only partial physics is included. In addition, we propose a novel transfer optimization scheme for use in such surrogate modeling scenarios and demonstrate an approximately 3x improvement in speed to convergence and an order of magnitude improvement in predictive performance over conventional Xavier initialization for training of new scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge