Implicit regularization for convex regularizers
Paper and Code
Jun 17, 2020
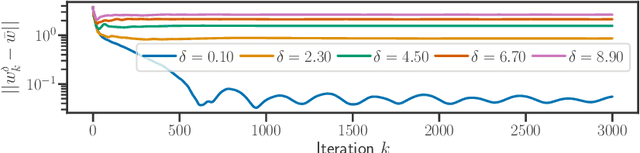
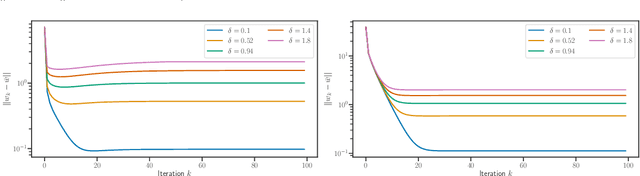
We study implicit regularization for over-parameterized linear models, when the bias is convex but not necessarily strongly convex. We characterize the regularization property of a primal-dual gradient based approach, analyzing convergence and especially stability in the presence of worst case deterministic noise. As a main example, we specialize and illustrate the results for the problem of robust sparse recovery. Key to our analysis is a combination of ideas from regularization theory and optimization in the presence of errors. Theoretical results are complemented by experiments showing that state-of-the-art performances are achieved with considerable computational speed-ups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge