Image Tag Completion by Low-rank Factorization with Dual Reconstruction Structure Preserved
Paper and Code
Jun 09, 2014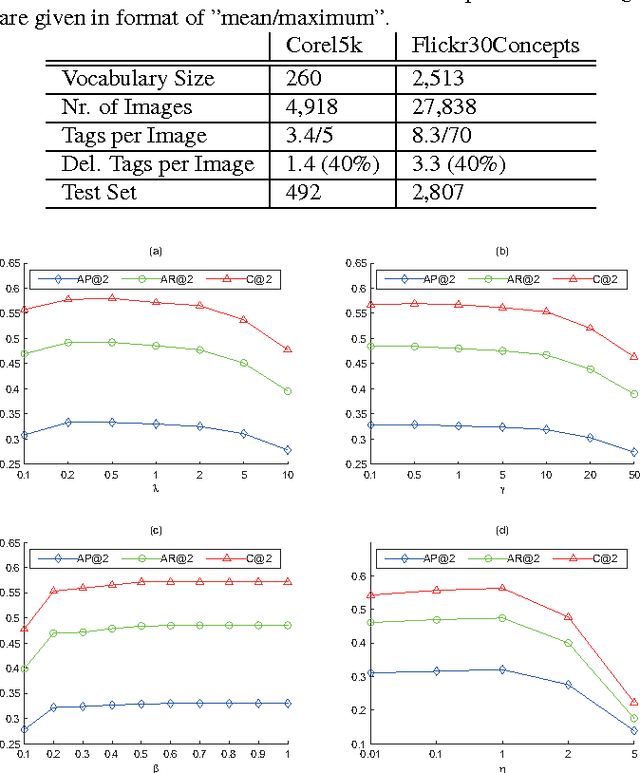
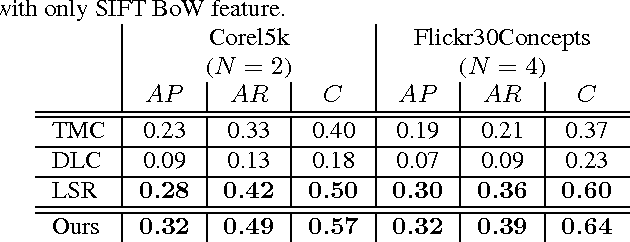
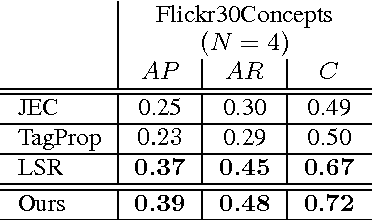
A novel tag completion algorithm is proposed in this paper, which is designed with the following features: 1) Low-rank and error s-parsity: the incomplete initial tagging matrix D is decomposed into the complete tagging matrix A and a sparse error matrix E. However, instead of minimizing its nuclear norm, A is further factor-ized into a basis matrix U and a sparse coefficient matrix V, i.e. D=UV+E. This low-rank formulation encapsulating sparse coding enables our algorithm to recover latent structures from noisy initial data and avoid performing too much denoising; 2) Local reconstruction structure consistency: to steer the completion of D, the local linear reconstruction structures in feature space and tag space are obtained and preserved by U and V respectively. Such a scheme could alleviate the negative effect of distances measured by low-level features and incomplete tags. Thus, we can seek a balance between exploiting as much information and not being mislead to suboptimal performance. Experiments conducted on Corel5k dataset and the newly issued Flickr30Concepts dataset demonstrate the effectiveness and efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge