iDARTS: Differentiable Architecture Search with Stochastic Implicit Gradients
Paper and Code
Jun 21, 2021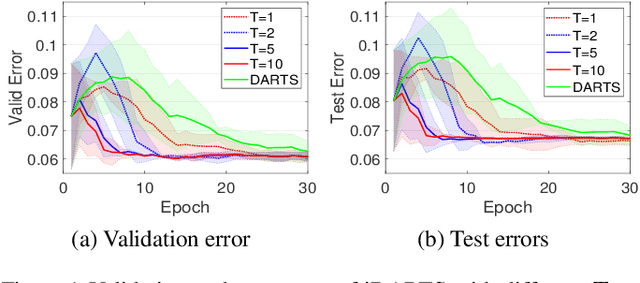
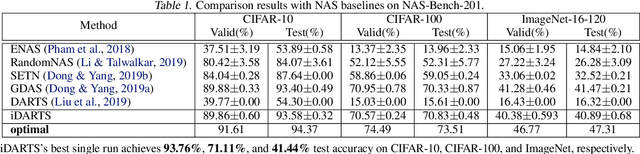
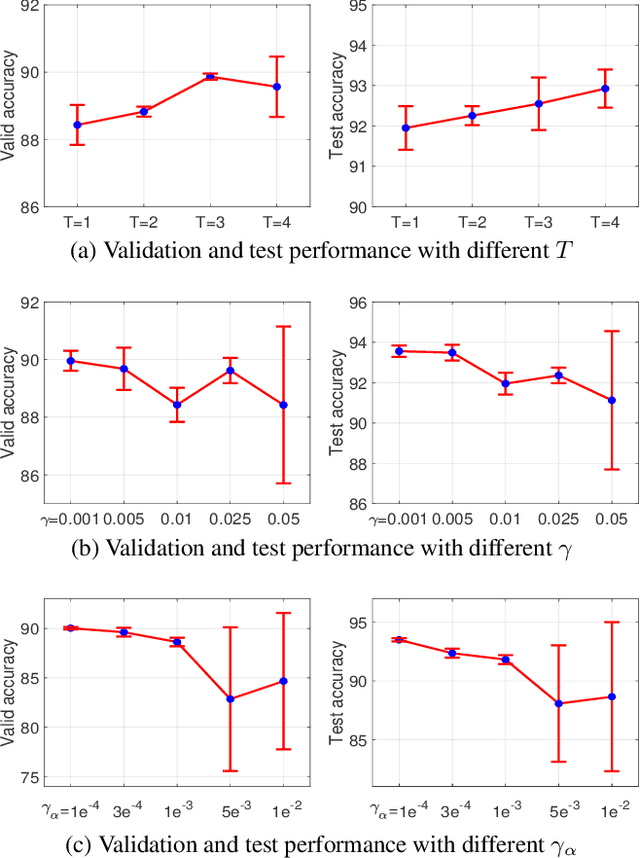
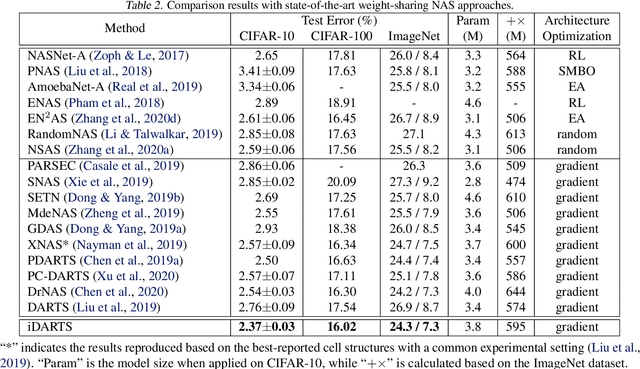
\textit{Differentiable ARchiTecture Search} (DARTS) has recently become the mainstream of neural architecture search (NAS) due to its efficiency and simplicity. With a gradient-based bi-level optimization, DARTS alternately optimizes the inner model weights and the outer architecture parameter in a weight-sharing supernet. A key challenge to the scalability and quality of the learned architectures is the need for differentiating through the inner-loop optimisation. While much has been discussed about several potentially fatal factors in DARTS, the architecture gradient, a.k.a. hypergradient, has received less attention. In this paper, we tackle the hypergradient computation in DARTS based on the implicit function theorem, making it only depends on the obtained solution to the inner-loop optimization and agnostic to the optimization path. To further reduce the computational requirements, we formulate a stochastic hypergradient approximation for differentiable NAS, and theoretically show that the architecture optimization with the proposed method, named iDARTS, is expected to converge to a stationary point. Comprehensive experiments on two NAS benchmark search spaces and the common NAS search space verify the effectiveness of our proposed method. It leads to architectures outperforming, with large margins, those learned by the baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge