Hyperspectral Image Denoising with Log-Based Robust PCA
Paper and Code
May 25, 2021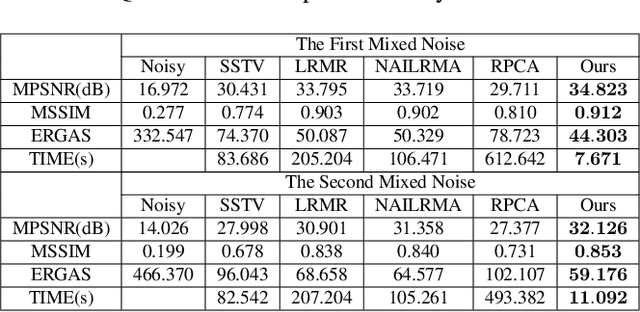


It is a challenging task to remove heavy and mixed types of noise from Hyperspectral images (HSIs). In this paper, we propose a novel nonconvex approach to RPCA for HSI denoising, which adopts the log-determinant rank approximation and a novel $\ell_{2,\log}$ norm, to restrict the low-rank or column-wise sparse properties for the component matrices, respectively.For the $\ell_{2,\log}$-regularized shrinkage problem, we develop an efficient, closed-form solution, which is named $\ell_{2,\log}$-shrinkage operator, which can be generally used in other problems. Extensive experiments on both simulated and real HSIs demonstrate the effectiveness of the proposed method in denoising HSIs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge