Hybrid Subspace Learning for High-Dimensional Data
Paper and Code
Aug 05, 2018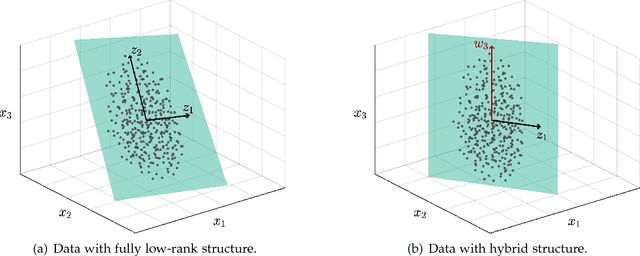
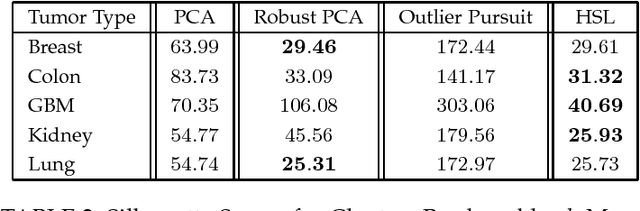
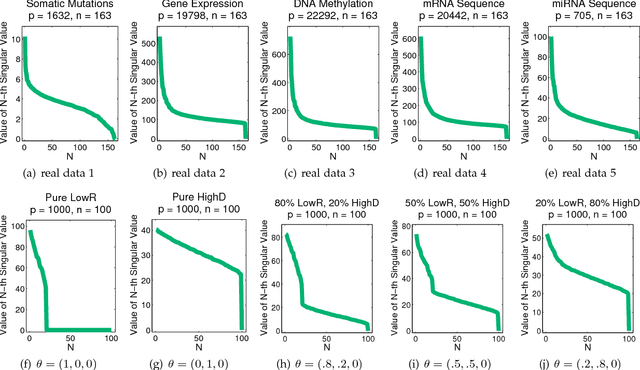
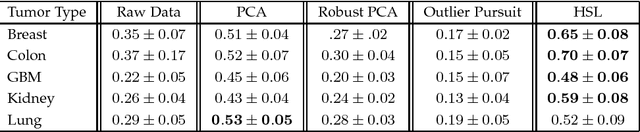
The high-dimensional data setting, in which p >> n, is a challenging statistical paradigm that appears in many real-world problems. In this setting, learning a compact, low-dimensional representation of the data can substantially help distinguish signal from noise. One way to achieve this goal is to perform subspace learning to estimate a small set of latent features that capture the majority of the variance in the original data. Most existing subspace learning models, such as PCA, assume that the data can be fully represented by its embedding in one or more latent subspaces. However, in this work, we argue that this assumption is not suitable for many high-dimensional datasets; often only some variables can easily be projected to a low-dimensional space. We propose a hybrid dimensionality reduction technique in which some features are mapped to a low-dimensional subspace while others remain in the original space. Our model leads to more accurate estimation of the latent space and lower reconstruction error. We present a simple optimization procedure for the resulting biconvex problem and show synthetic data results that demonstrate the advantages of our approach over existing methods. Finally, we demonstrate the effectiveness of this method for extracting meaningful features from both gene expression and video background subtraction datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge