How Does SimSiam Avoid Collapse Without Negative Samples? A Unified Understanding with Self-supervised Contrastive Learning
Paper and Code
Mar 30, 2022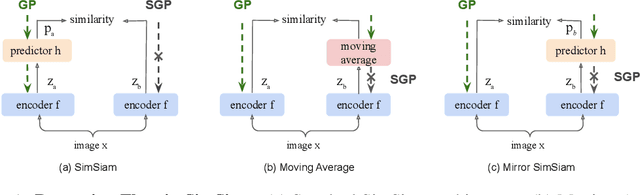
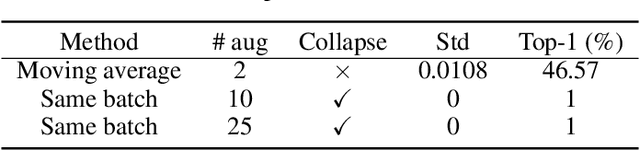

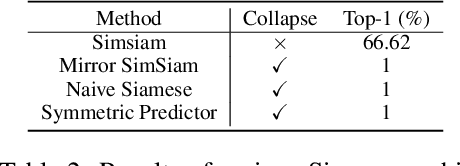
To avoid collapse in self-supervised learning (SSL), a contrastive loss is widely used but often requires a large number of negative samples. Without negative samples yet achieving competitive performance, a recent work has attracted significant attention for providing a minimalist simple Siamese (SimSiam) method to avoid collapse. However, the reason for how it avoids collapse without negative samples remains not fully clear and our investigation starts by revisiting the explanatory claims in the original SimSiam. After refuting their claims, we introduce vector decomposition for analyzing the collapse based on the gradient analysis of the $l_2$-normalized representation vector. This yields a unified perspective on how negative samples and SimSiam alleviate collapse. Such a unified perspective comes timely for understanding the recent progress in SSL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge