Hard instance learning for quantum adiabatic prime factorization
Paper and Code
Oct 10, 2021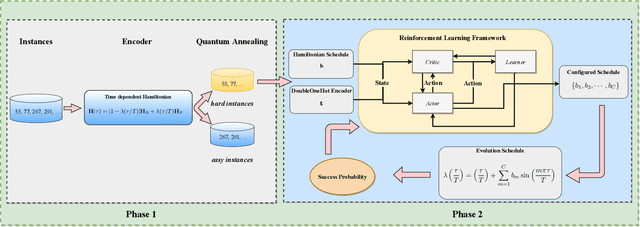
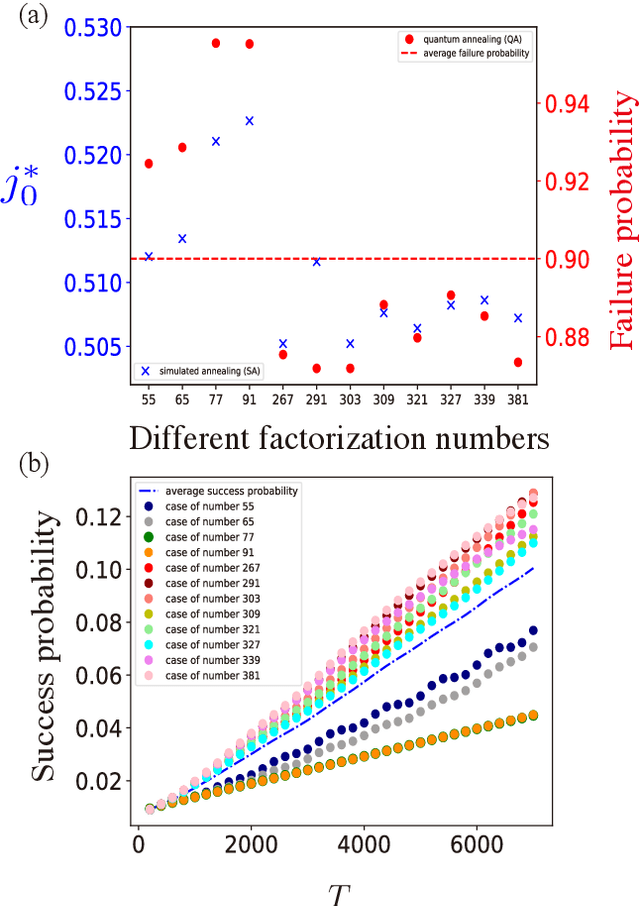
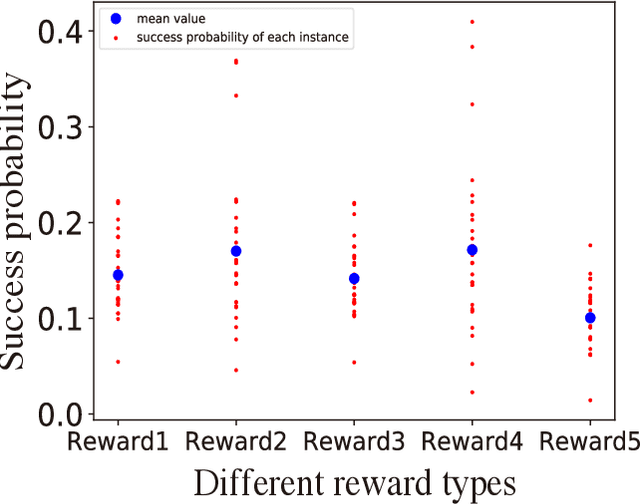
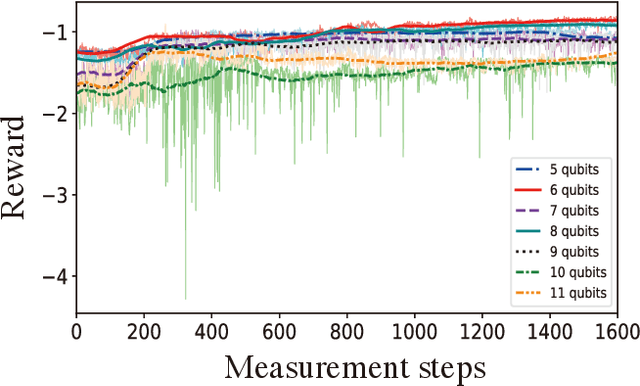
Prime factorization is a difficult problem with classical computing, whose exponential hardness is the foundation of Rivest-Shamir-Adleman (RSA) cryptography. With programmable quantum devices, adiabatic quantum computing has been proposed as a plausible approach to solve prime factorization, having promising advantage over classical computing. Here, we find there are certain hard instances that are consistently intractable for both classical simulated annealing and un-configured adiabatic quantum computing (AQC). Aiming at an automated architecture for optimal configuration of quantum adiabatic factorization, we apply a deep reinforcement learning (RL) method to configure the AQC algorithm. By setting the success probability of the worst-case problem instances as the reward to RL, we show the AQC performance on the hard instances is dramatically improved by RL configuration. The success probability also becomes more evenly distributed over different problem instances, meaning the configured AQC is more stable as compared to the un-configured case. Through a technique of transfer learning, we find prominent evidence that the framework of AQC configuration is scalable -- the configured AQC as trained on five qubits remains working efficiently on nine qubits with a minimal amount of additional training cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge