Growing Better Graphs With Latent-Variable Probabilistic Graph Grammars
Paper and Code
Jun 11, 2018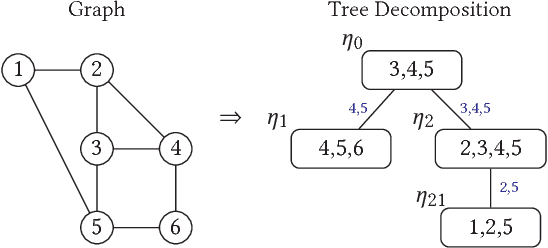
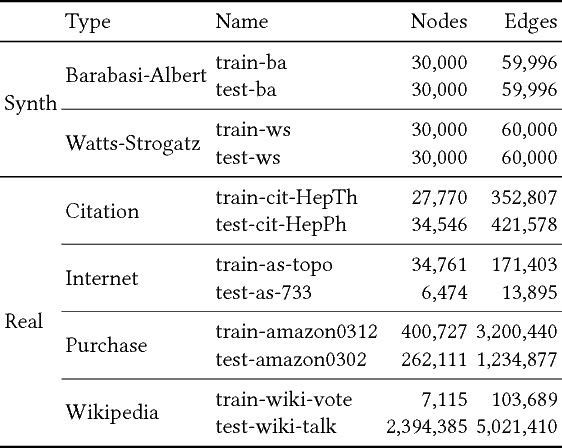
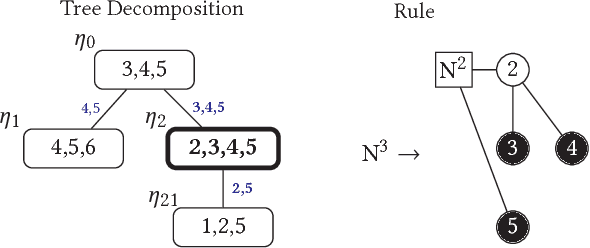
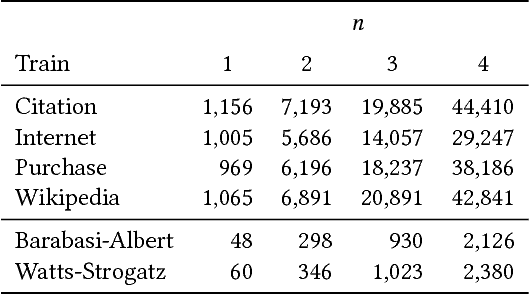
Recent work in graph models has found that probabilistic hyperedge replacement grammars (HRGs) can be extracted from graphs and used to generate new random graphs with graph properties and substructures close to the original. In this paper, we show how to add latent variables to the model, trained using Expectation-Maximization, to generate still better graphs, that is, ones that generalize better to the test data. We evaluate the new method by separating training and test graphs, building the model on the former and measuring the likelihood of the latter, as a more stringent test of how well the model can generalize to new graphs. On this metric, we find that our latent-variable HRGs consistently outperform several existing graph models and provide interesting insights into the building blocks of real world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge