Group Preserving Label Embedding for Multi-Label Classification
Paper and Code
Dec 24, 2018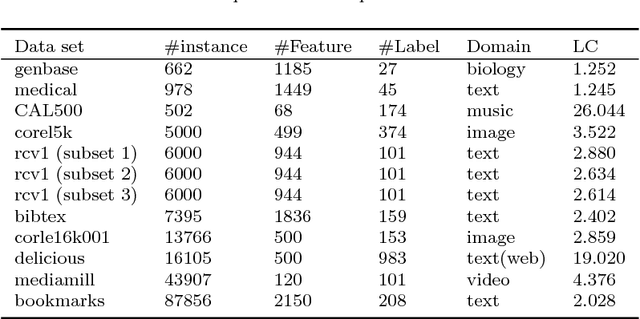
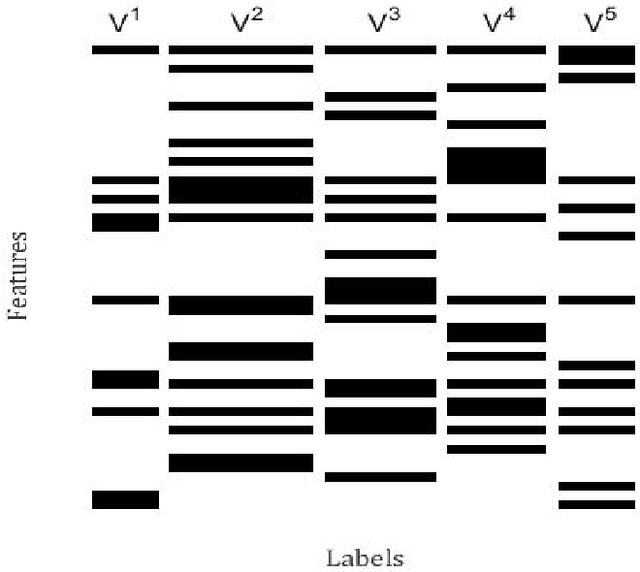
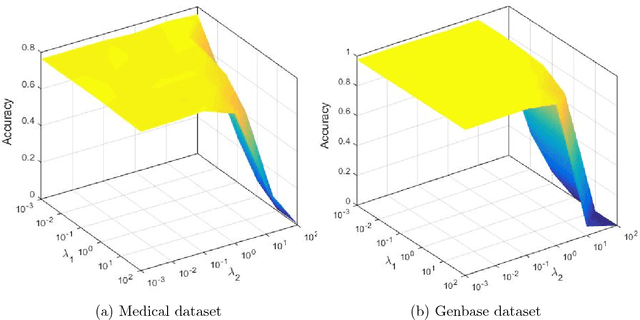

Multi-label learning is concerned with the classification of data with multiple class labels. This is in contrast to the traditional classification problem where every data instance has a single label. Due to the exponential size of output space, exploiting intrinsic information in feature and label spaces has been the major thrust of research in recent years and use of parametrization and embedding have been the prime focus. Researchers have studied several aspects of embedding which include label embedding, input embedding, dimensionality reduction and feature selection. These approaches differ from one another in their capability to capture other intrinsic properties such as label correlation, local invariance etc. We assume here that the input data form groups and as a result, the label matrix exhibits a sparsity pattern and hence the labels corresponding to objects in the same group have similar sparsity. In this paper, we study the embedding of labels together with the group information with an objective to build an efficient multi-label classification. We assume the existence of a low-dimensional space onto which the feature vectors and label vectors can be embedded. In order to achieve this, we address three sub-problems namely; (1) Identification of groups of labels; (2) Embedding of label vectors to a low rank-space so that the sparsity characteristic of individual groups remains invariant; and (3) Determining a linear mapping that embeds the feature vectors onto the same set of points, as in stage 2, in the low-dimensional space. We compare our method with seven well-known algorithms on twelve benchmark data sets. Our experimental analysis manifests the superiority of our proposed method over state-of-art algorithms for multi-label learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge